Difference between revisions of "Moment"
| Line 195: | Line 195: | ||
<math>F = 100N</math> | <math>F = 100N</math> | ||
|} | |} | ||
| + | |||
| + | ===References=== | ||
| + | ====AQA==== | ||
| + | |||
| + | :[https://www.amazon.co.uk/gp/product/0008158770/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=0008158770&linkCode=as2&tag=nrjc-21&linkId=ec31595e720e1529e49876c3866fff6e ''Moment, pages 168-9, GCSE Physics; Student Book, Collins, AQA ''] | ||
| + | :[https://www.amazon.co.uk/gp/product/178294558X/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=178294558X&linkCode=as2&tag=nrjc-21&linkId=f0dfb66dafcb0c6e9449e7b1a4ae1ac317 ''Moments, page 57, GCSE Physics; The Revision Guide, CGP, AQA ''] | ||
| + | :[https://www.amazon.co.uk/gp/product/019835939X/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=019835939X&linkCode=as2&tag=nrjc-21&linkId=57e96876985fc39b1a3d8a3e3dc238b6 ''Moments, pages 120-123, 126-127, GCSE Physics; Third Edition, Oxford University Press, AQA ''] | ||
| + | :[https://www.amazon.co.uk/gp/product/1782945970/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945970&linkCode=as2&tag=nrjc-21&linkId=a120d24dcc7cc7a58192069a3aafc1d2 ''Moments, pages 165, 166, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA ''] | ||
Revision as of 17:48, 8 November 2019
Contents
Key Stage 3
Meaning
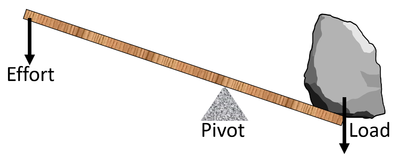
A moment is the turning effect of a force.
About Moments
- When a force acts on an object with a pivot it becomes a turning force called a moment.
- A moment can be calculated by multiplying a force by the distance from a pivot.
- The units of a moment are Newton Metres (Nm).
- Moments can be used to make Force Multipliers using a pivot and lever.
- The longer the lever, the larger the moment that can be produced.
| Using moments an effort can be used to lift a load. If the pivot is closer to the load than the effort then the force of effort can be smaller than the load to lift the object. |
Equation
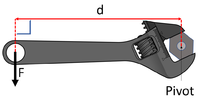
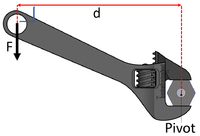
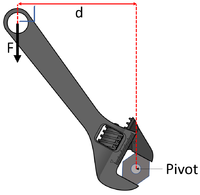
Moment = Force x Perpendicular distance from the pivot.
\(M = F \times d\)
Where:
- M = Moment
- F = Force
- d = Perpendicular distance from the pivot.
Example Calculations
| A 20N force of effort is applied at a perpendicular distance of 0.15m from the pivot. Calculate the Moment. | A 20N force of effort is applied at a perpendicular distance of 14cm from the pivot. Calculate the Moment. | A 20N force of effort is applied at a perpendicular distance of 100mm from the pivot. Calculate the Moment. |
|
Force = 20N Perpendicular distance = 0.15m \(M = F \times d\) \(M = 20 \times 0.15\) \(M = 3.0Nm\) |
Force = 20N Perpendicular distance = 14cm = 0.14m \(M = F \times d\) \(M = 20 \times 0.14\) \(M = 2.8Nm\) |
Force = 20N Perpendicular distance = 100mm = 0.10m \(M = F \times d\) \(M = 20 \times 0.10\) \(M = 2.0Nm\) |
Extra Information
Key Stage 4
Meaning
A moment is the turning effect of a force.
About Moments
- When a force acts on an object with a pivot it becomes a turning force called a moment.
- A moment can be calculated by multiplying a force by the distance from a pivot.
- The units of a moment are Newton Metres (Nm).
- Moments can be used to make Force Multipliers using a pivot and lever.
- The longer the lever, the larger the moment that can be produced.
| Using moments an effort can be used to lift a load. If the pivot is closer to the load than the effort then the force of effort can be smaller than the load to lift the object. |
Equation
Moment = Force x Perpendicular distance from the pivot.
\(M = F \times d\)
Where:
- M = Moment
- F = Force
- d = Perpendicular distance from the pivot.
Example Calculations
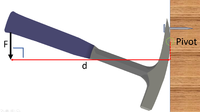
| A hammer is used to pull out a nail from a wall. A 30N force of effort is applied at a perpendicular distance of 0.18m from the pivot. While the nail is 0.02m away from the pivot. Calculate the force applied to the nail at this point. | A hammer is used to pull out a nail from a wall. A 30N force of effort is applied at a perpendicular distance of 19cm from the pivot. While the nail is 4cm away from the pivot. Calculate the force applied to the nail at this point. | A hammer is used to pull out a nail from a wall. A 30N force of effort is applied at a perpendicular distance of 200mm from the pivot. While the nail is 60mm away from the pivot. Calculate the force applied to the nail at this point. |
| A 30N force of effort is applied at a perpendicular distance of 0.18m from the pivot. Calculate the Moment. | A 30N force of effort is applied at a perpendicular distance of 19cm from the pivot. Calculate the Moment. | A 30N force of effort is applied at a perpendicular distance of 200mm from the pivot. Calculate the Moment. |
| 1. State the known quantities
Force = 30N Perpendicular distance between effort and pivot = 0.18m Perpendicular distance between effort and pivot = 0.02m |
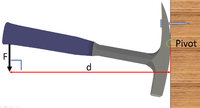
1. State the known quantities
Force = 30N Perpendicular distance between effort and pivot = 19cm = 0.19m Perpendicular distance between effort and pivot = 4cm = 0.04m |
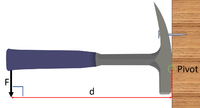
1. State the known quantities
Force = 30N Perpendicular distance between effort and pivot = 200mm = 0.200m Perpendicular distance between effort and pivot = 60mm = 0.06m |
| 2. Find the moment caused by the effort.
\(M = F \times d\) \(M = 30 \times 0.18\) \(M = 5.4Nm\) |
2. Find the moment caused by the effort.
\(M = F \times d\) \(M = 30 \times 0.19\) \(M = 5.7Nm\) |
2. Find the moment caused by the effort.
\(M = F \times d\) \(M = 30 \times 0.20\) \(M = 6.0Nm\) |
| 3. Calculate the Force applied to the nail from the moment.
Moment = 5.4Nm Perpendicular distance = 0.02m \(M = F \times d\) \(5.4 = F \times 0.02\) \(F = \frac{5.4}{0.02}\) \(F = 270N\) |
3. Calculate the Force applied to the nail from the moment.
Moment = 5.7Nm Perpendicular distance = 4cm = 0.04m \(M = F \times d\) \(5.7 = F \times 0.04\) \(F = \frac{5.7}{0.04}\) \(F = 142.5N\) |
3. Calculate the Force applied to the nail from the moment.
Moment = 6.0Nm Perpendicular distance = 60mm = 0.06m \(M = F \times d\) \(6.0 = F \times 0.06\) \(F = \frac{6.0}{0.06}\) \(F = 100N\) |