Difference between revisions of "Moment"
(→Example Calculations) |
|||
| Line 6: | Line 6: | ||
: When a [[force]] acts on an [[object]] with a [[pivot]] it becomes a turning force called a [[moment]]. | : When a [[force]] acts on an [[object]] with a [[pivot]] it becomes a turning force called a [[moment]]. | ||
: A '''moment''' can be calculated by multiplying a [[force]] by the [[distance]] from a [[pivot]]. | : A '''moment''' can be calculated by multiplying a [[force]] by the [[distance]] from a [[pivot]]. | ||
| + | : The [[unit]]s of a '''moment''' are [[Newton Metre]]s (Nm). | ||
: '''Moment'''s can be used to make [[Force Multiplier]]s using a [[pivot]] and [[lever]]. | : '''Moment'''s can be used to make [[Force Multiplier]]s using a [[pivot]] and [[lever]]. | ||
: The longer the lever, the larger the [[moment]] that can be produced. | : The longer the lever, the larger the [[moment]] that can be produced. | ||
| Line 36: | Line 37: | ||
|[[File:MomentSpanner3.png|center|200px]] | |[[File:MomentSpanner3.png|center|200px]] | ||
|- | |- | ||
| − | | style="height:20px; width:200px; text-align:left;" | | + | | style="height:20px; width:200px; text-align:left;" | |
| − | | style="height:20px; width:200px; text-align:left;" | | + | Force = 20N |
| − | | style="height:20px; width:200px; text-align:left;" | | + | |
| + | Perpendicular distance = 0.15m | ||
| + | |||
| + | <math>M = F \times d</math> | ||
| + | |||
| + | <math>M = 20 \times 0.15</math> | ||
| + | |||
| + | <math>M = 3.0Nm</math> | ||
| + | | style="height:20px; width:200px; text-align:left;" | | ||
| + | Force = 20N | ||
| + | |||
| + | Perpendicular distance = 14cm = 0.14m | ||
| + | |||
| + | <math>M = F \times d</math> | ||
| + | |||
| + | <math>M = 20 \times 0.14</math> | ||
| + | |||
| + | <math>M = 2.8Nm</math> | ||
| + | | style="height:20px; width:200px; text-align:left;" | | ||
| + | Force = 20N | ||
| + | |||
| + | Perpendicular distance = 100mm = 0.10m | ||
| + | |||
| + | <math>M = F \times d</math> | ||
| + | |||
| + | <math>M = 20 \times 0.10</math> | ||
| + | |||
| + | <math>M = 2.0Nm</math> | ||
|- | |- | ||
|[[File:MomentHammer1.png|center|200px]] | |[[File:MomentHammer1.png|center|200px]] | ||
Revision as of 09:26, 14 October 2018
Key Stage 3
Meaning
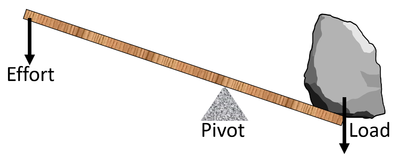
A moment is the turning effect of a force.
About Moments
- When a force acts on an object with a pivot it becomes a turning force called a moment.
- A moment can be calculated by multiplying a force by the distance from a pivot.
- The units of a moment are Newton Metres (Nm).
- Moments can be used to make Force Multipliers using a pivot and lever.
- The longer the lever, the larger the moment that can be produced.
| Using moments an effort can be used to lift a load. If the pivot is closer to the load than the effort then the force of effort can be smaller than the load to lift the object. |
Equation
Moment = Force x Perpendicular distance from the pivot.
\[M = F \times d\] Where:
- M = Moment
- F = Force
- d = Perpendicular distance from the pivot.
Example Calculations
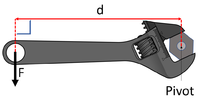
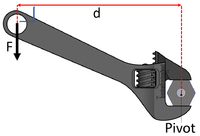
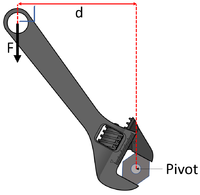
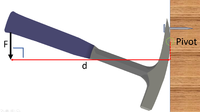
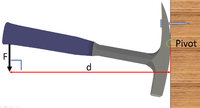
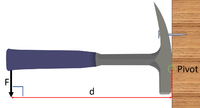
| A 20N force of effort is applied at a perpendicular distance of 0.15m from the pivot. Calculate the Moment. | A 20N force of effort is applied at a perpendicular distance of 14cm from the pivot. Calculate the Moment. | A 20N force of effort is applied at a perpendicular distance of 100mm from the pivot. Calculate the Moment. |
|
Force = 20N Perpendicular distance = 0.15m \(M = F \times d\) \(M = 20 \times 0.15\) \(M = 3.0Nm\) |
Force = 20N Perpendicular distance = 14cm = 0.14m \(M = F \times d\) \(M = 20 \times 0.14\) \(M = 2.8Nm\) |
Force = 20N Perpendicular distance = 100mm = 0.10m \(M = F \times d\) \(M = 20 \times 0.10\) \(M = 2.0Nm\) |
| Text | Text | Text |