Difference between revisions of "Frequency"
(→Example Calculations) |
|||
| Line 70: | Line 70: | ||
===Example Calculations=== | ===Example Calculations=== | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | | style="height:20px; width: | + | | style="height:20px; width:300px; text-align:center;" |A scientist wants to determine the [[frequency]] of a [[pendulum]]. They count that the [[pendulum]] [[oscillate]]s 15 times over 20 seconds. Calculate the [[frequency]] of the [[pendulum]]. |
| − | | style="height:20px; width: | + | | style="height:20px; width:300px; text-align:center;" |A sailor notices a buoy bounce up and down 24 times over a minute. Calculate the [[frequency]] of the [[wave]]s. |
|- | |- | ||
| − | | style="height:20px; width: | + | | style="height:20px; width:300px; text-align:left;" |'''1. State the known quantities''' |
n = 15 | n = 15 | ||
t = 20s | t = 20s | ||
| − | | style="height:20px; width: | + | | style="height:20px; width:300px; text-align:left;" |'''1. State the known quantities''' |
n = 24 | n = 24 | ||
| Line 84: | Line 84: | ||
t = 60 | t = 60 | ||
|- | |- | ||
| − | | style="height:20px; width: | + | | style="height:20px; width:300px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' |
<math>f = \tfrac{n}{t}</math> | <math>f = \tfrac{n}{t}</math> | ||
| Line 92: | Line 92: | ||
<math>f = 0.75Hz</math> | <math>f = 0.75Hz</math> | ||
| − | | style="height:20px; width: | + | | style="height:20px; width:300px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' |
<math>f = \tfrac{n}{t}</math> | <math>f = \tfrac{n}{t}</math> | ||
Revision as of 13:13, 18 February 2019
Contents
Key Stage 3
Meaning
Frequency is the number of waves that pass by in one second.
About Frequency
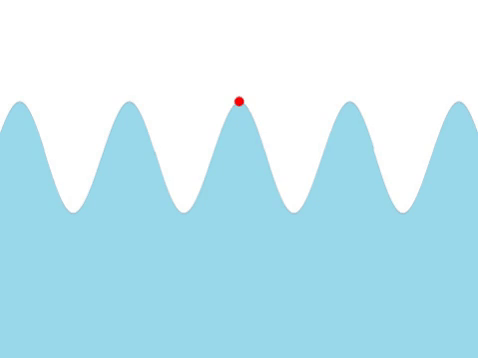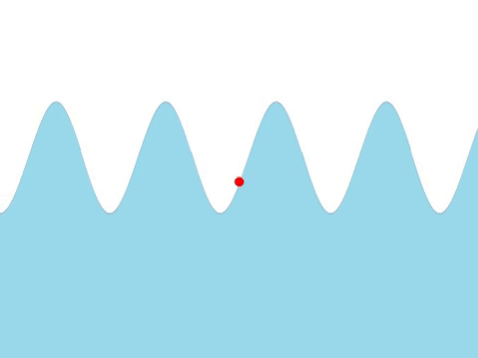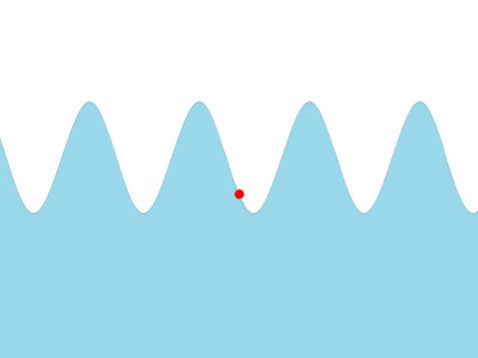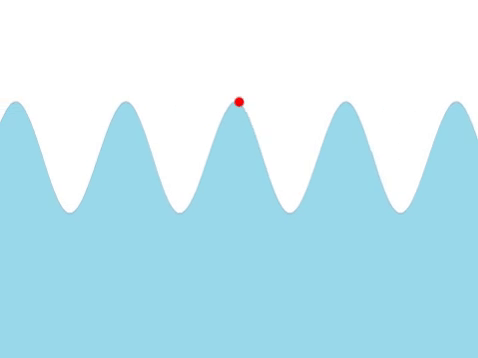
| Water Waves |
| The frequency of this wave can be found by counting the number of times the red marker oscillates every second. |
- The higher the frequency the quicker the wave oscillates.
- In sound frequency is known as pitch. A high pitch is a high frequency.
- In light frequency affects the colour of the light. Red is a low frequency and violet is a high frequency.
Equation
\(f = \tfrac{1}{T}\) Where:
- f = frequency
- T = time period (the time it takes for one wave to pass a point).
Key Stage 4
Meaning
Frequency is the number of waves that pass a given point in one second.
About Frequency
| Water Waves |
| The frequency of this wave can be found by counting the number of times the red marker oscillates every second. |
- The higher the frequency the quicker the wave oscillates.
- In sound frequency is known as pitch. A high pitch is a high frequency.
- In light frequency affects the colour of the light. Red is a low frequency and violet is a high frequency.
- Frequency can be found by counting the number of waves which pass a point in a given time and dividing this by the time.
Equation
NB: You do not need to remember these equations but you should know how to find frequency given the number of waves passing a point and the time taken.
Equation 1
Frequency = 1/(Period)
\(f = \tfrac{1}{T}\)
Where: f = Frequency
T = time period (the time it takes for a wave to pass a point).
Equation 2
Frequency = (Number of Waves which pass a point)/(Time taken for waves to pass a point)
\(f = \tfrac{n}{t}\)
Where: f = Frequency
n = Number of waves which pass a point.
t = The time taken for those waves to pass a point.
Example Calculations
| A scientist wants to determine the frequency of a pendulum. They count that the pendulum oscillates 15 times over 20 seconds. Calculate the frequency of the pendulum. | A sailor notices a buoy bounce up and down 24 times over a minute. Calculate the frequency of the waves. |
| 1. State the known quantities
n = 15 t = 20s |
1. State the known quantities
n = 24 t = 60 |
| 2. Substitute the numbers into the equation and solve.
\(f = \tfrac{n}{t}\) \(f = \tfrac{15}{20}\) \(f = 0.75Hz\) |
2. Substitute the numbers into the equation and solve.
\(f = \tfrac{n}{t}\) \(f = \tfrac{24}{60}\) \(f = 0.4Hz\) |