Difference between revisions of "Work Done"
(→Work Done on a Spring) |
|||
| Line 14: | Line 14: | ||
===Example Calculations=== | ===Example Calculations=== | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:center;" |'''A person lifts a 40N box by a height of 1.2m. Calculate the work done by the person against gravity.''' | ||
| + | | style="height:20px; width:200px; text-align:center;" |'''The brakes on a car apply a force of 10,000N. The car travels a distance of 15m braking. Calculate the work done by the brakes.''' | ||
| + | | style="height:20px; width:200px; text-align:center;" |'''A person carries a 20N box along a horizontal path of 20m.''' | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:left;" | | ||
| + | Force = 40N | ||
| + | |||
| + | Distance moved in the direction of the force = 1.2m | ||
| + | |||
| + | <math> W = Fd</math> | ||
| + | |||
| + | <math> W = 40 \times 1.2</math> | ||
| + | |||
| + | <math> W = 48J</math> | ||
| + | | style="height:20px; width:200px; text-align:left;" | | ||
| + | Force = 10,000N | ||
| + | |||
| + | Distance moved in the direction of the force = 15m | ||
| + | |||
| + | <math> W = Fd</math> | ||
| + | |||
| + | <math> W = 10,000 \times 15</math> | ||
| + | |||
| + | <math> W = 15,000J</math> | ||
| + | | style="height:20px; width:200px; text-align:left;" | | ||
| + | Force = 40N | ||
| + | |||
| + | Distance moved in the direction of the force = 0m | ||
| + | |||
| + | <math> W = Fd</math> | ||
| + | |||
| + | <math> W = 20 \times 0</math> | ||
| + | |||
| + | <math> W = 0J</math> | ||
| + | |||
| + | No '''work''' has been done because the movement is not in the direction of the [[force]]. The [[weight]] acts downwards but the movement was horizontal. | ||
| + | |} | ||
| + | |||
: 1. A person lifts a 40N box by a height of 1.2m. Calculate the work done by the person against gravity. | : 1. A person lifts a 40N box by a height of 1.2m. Calculate the work done by the person against gravity. | ||
: Force = 40N | : Force = 40N | ||
Revision as of 10:22, 14 October 2018
Contents
Key Stage 3
Meaning
Work Done is the amount of energy transferred by the action of a force.
About Work Done
- Work Done is measured in Joules.
- Work Done can only be calculated for objects moving in the direction of the force.
Equation
Work Done = Force X Distance moved in the direction of the force \[ W = F \times d\] \[ W = Fd\]
- Work done is written with a capital W. Force is written with a capital F. Distance is written with a lower case d.
Example Calculations
| A person lifts a 40N box by a height of 1.2m. Calculate the work done by the person against gravity. | The brakes on a car apply a force of 10,000N. The car travels a distance of 15m braking. Calculate the work done by the brakes. | A person carries a 20N box along a horizontal path of 20m. |
|
Force = 40N Distance moved in the direction of the force = 1.2m \( W = Fd\) \( W = 40 \times 1.2\) \( W = 48J\) |
Force = 10,000N Distance moved in the direction of the force = 15m \( W = Fd\) \( W = 10,000 \times 15\) \( W = 15,000J\) |
Force = 40N Distance moved in the direction of the force = 0m \( W = Fd\) \( W = 20 \times 0\) \( W = 0J\) No work has been done because the movement is not in the direction of the force. The weight acts downwards but the movement was horizontal. |
- 1. A person lifts a 40N box by a height of 1.2m. Calculate the work done by the person against gravity.
- Force = 40N
- Distance moved in the direction of the force = 1.2m
\[ W = Fd\] \[ W = 40 \times 1.2\] \[ W = 48J\]
- 2. The brakes on a car apply a force of 10,000N. The car travels a distance of 15m braking. Calculate the work done by the brakes.
- Force = 10,000N
- Distance moved in the direction of the force = 15m
\[ W = Fd\] \[ W = 10,000 \times 15\] \[ W = 15,000J\]
- 3. A person carries a 20N box along a horizontal path of 20m.
- Force = 40N
- Distance moved in the direction of the force = 0m
\[ W = Fd\] \[ W = 20 \times 0\] \[ W = 0J\] No work has been done because the movement is not in the direction of the force. The weight acts downwards but the movement was horizontal.
Work Done by Deformation
- When an object is deformed, such as a spring being stretched, work is done to transfer energy into its Elastic Potential Energy Store.
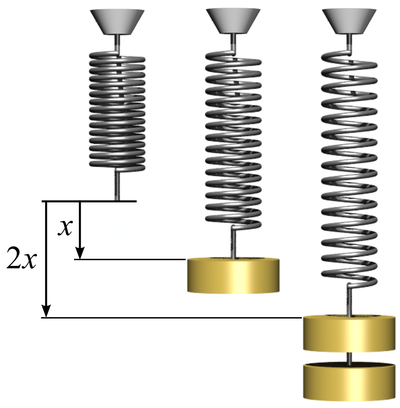
Work Done on a Spring
| Work is done to stretch this spring. |
- The Force needed to stretch a spring is proportional to the extension of the spring (Hooke's Law). Force = Spring Constant x Extension
- The Work Done on an object is proportional to the force and the distance traveled. Work Done = Force x Distance
- The distance moved is the same as the extension 'x'.
These two equations can be combined:
- 1. \( F = kx\)
- 2. \( W = Fx\)
Substitute 1 into 2. \[W = (kx) \times x\] \[W = kx^2\]