Difference between revisions of "Frequency"
| Line 11: | Line 11: | ||
|[[File:WaveFrequency.gif|center]] | |[[File:WaveFrequency.gif|center]] | ||
|- | |- | ||
| − | | style="height:20px; width:200px; text-align:center;" |The [[frequency]] of this [[wave]] can be found by counting the number of times the red marker | + | | style="height:20px; width:200px; text-align:center;" |The [[frequency]] of this [[wave]] can be found by counting the number of times the red marker [[oscillate]]s every [[second]]. |
|} | |} | ||
: The higher the [[frequency]] the quicker the [[wave]] [[Oscillation|oscillates]]. | : The higher the [[frequency]] the quicker the [[wave]] [[Oscillation|oscillates]]. | ||
| Line 20: | Line 20: | ||
<math>f = \tfrac{1}{T}</math> | <math>f = \tfrac{1}{T}</math> | ||
Where: | Where: | ||
| − | : f = frequency | + | : f = [[frequency]] |
| − | : T = time period (the time it takes for a wave to pass a point). | + | : T = [[Period|time period]] (the [[time]] it takes for one [[wave]] to pass a point). |
| + | |||
| + | ==Key Stage 4== | ||
| + | ===Meaning=== | ||
| + | [[Frequency]] is the number of [[wave]]s that pass a given point in one [[second]]. | ||
| + | |||
| + | ===About Frequency=== | ||
| + | : [[Frequency]] is [[measure]]d in [[Hertz]] ([[Hz]]). | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:center;" |'''Water Waves''' | ||
| + | |- | ||
| + | |[[File:WaveFrequency.gif|center]] | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:center;" |The [[frequency]] of this [[wave]] can be found by counting the number of times the red marker [[oscillate]]s every [[second]]. | ||
| + | |} | ||
| + | : The higher the [[frequency]] the quicker the [[wave]] [[Oscillation|oscillates]]. | ||
| + | : In [[sound]] [[frequency]] is known as [[pitch]]. A high [[pitch]] is a high [[frequency]]. | ||
| + | : In [[light]] [[frequency]] affects the [[colour]] of the [[light]]. Red is a low [[frequency]] and violet is a high [[frequency]]. | ||
| + | : [[Frequency]] can be found by counting the number of [[wave]]s which pass a point in a given [[time]] and dividing this by the [[time]]. | ||
| + | |||
| + | ===Equation=== | ||
| + | ''NB: You do not need to remember these equations but you should know how to find [[frequency]] given the number of waves passing a point and the time taken.'' | ||
| + | |||
| + | ====Equation 1==== | ||
| + | Frequency = 1/(Period) | ||
| + | |||
| + | <math>f = \tfrac{1}{T}</math> | ||
| + | |||
| + | Where: | ||
| + | f = [[Frequency]] | ||
| + | |||
| + | T = [[Period|time period]] (the [[time]] it takes for a wave to pass a point). | ||
| + | |||
| + | ====Equation 2==== | ||
| + | |||
| + | Frequency = (Number of Waves which pass a point)/(Time taken for waves to pass a point) | ||
| + | |||
| + | <math>f = \tfrac{n}{t}</math> | ||
| + | |||
| + | Where: | ||
| + | f = [[Frequency]] | ||
| + | |||
| + | n = Number of [[wave]]s which pass a point. | ||
| + | |||
| + | t = The [[time]] taken for those [[wave]]s to pass a point. | ||
| + | |||
| + | ===Example Calculations=== | ||
| + | {| class="wikitable" | ||
| + | | style="height:20px; width:200px; text-align:center;" |A scientist wants to determine the [[frequency]] of a [[pendulum]]. They count that the [[pendulum]] [[oscillate]]s 15 times over 20 seconds. Calculate the [[frequency]] of the [[pendulum]]. | ||
| + | | style="height:20px; width:200px; text-align:center;" |A sailor notices a buoy bounce up and down 24 times over a minute. Calculate the [[frequency]] of the [[wave]]s. | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities''' | ||
| + | |||
| + | n = 15 | ||
| + | |||
| + | t = 20s | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities''' | ||
| + | |||
| + | n = 24 | ||
| + | |||
| + | t = 60 | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math>f = \tfrac{n}{t}</math> | ||
| + | |||
| + | <math>f = \tfrac{15}{20}</math> | ||
| + | |||
| + | <math>f = 0.75Hz</math> | ||
| + | |||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math>f = \tfrac{n}{t}</math> | ||
| + | |||
| + | <math>f = \tfrac{24}{60}</math> | ||
| + | |||
| + | <math>f = 0.4Hz</math> | ||
| + | |} | ||
Revision as of 13:13, 18 February 2019
Contents
Key Stage 3
Meaning
Frequency is the number of waves that pass by in one second.
About Frequency
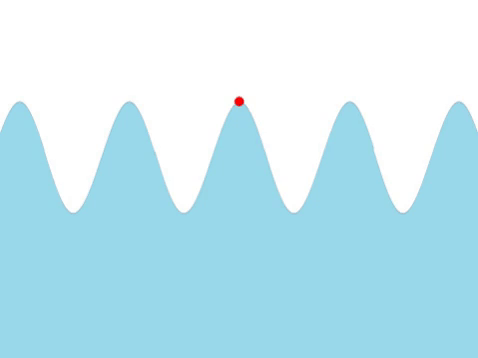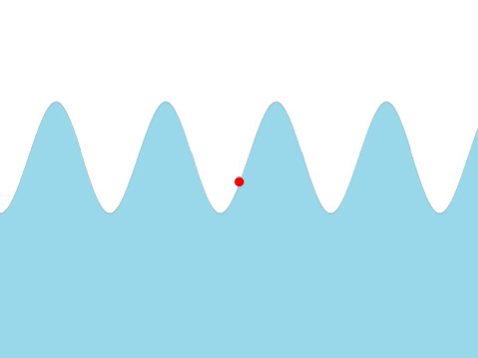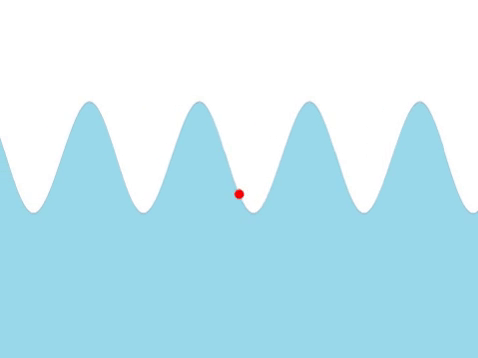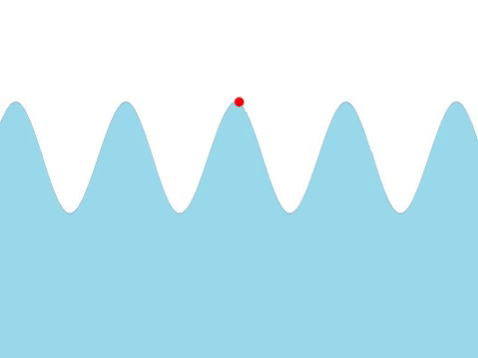
| Water Waves |
| The frequency of this wave can be found by counting the number of times the red marker oscillates every second. |
- The higher the frequency the quicker the wave oscillates.
- In sound frequency is known as pitch. A high pitch is a high frequency.
- In light frequency affects the colour of the light. Red is a low frequency and violet is a high frequency.
Equation
\(f = \tfrac{1}{T}\) Where:
- f = frequency
- T = time period (the time it takes for one wave to pass a point).
Key Stage 4
Meaning
Frequency is the number of waves that pass a given point in one second.
About Frequency
| Water Waves |
| The frequency of this wave can be found by counting the number of times the red marker oscillates every second. |
- The higher the frequency the quicker the wave oscillates.
- In sound frequency is known as pitch. A high pitch is a high frequency.
- In light frequency affects the colour of the light. Red is a low frequency and violet is a high frequency.
- Frequency can be found by counting the number of waves which pass a point in a given time and dividing this by the time.
Equation
NB: You do not need to remember these equations but you should know how to find frequency given the number of waves passing a point and the time taken.
Equation 1
Frequency = 1/(Period)
\(f = \tfrac{1}{T}\)
Where: f = Frequency
T = time period (the time it takes for a wave to pass a point).
Equation 2
Frequency = (Number of Waves which pass a point)/(Time taken for waves to pass a point)
\(f = \tfrac{n}{t}\)
Where: f = Frequency
n = Number of waves which pass a point.
t = The time taken for those waves to pass a point.
Example Calculations
| A scientist wants to determine the frequency of a pendulum. They count that the pendulum oscillates 15 times over 20 seconds. Calculate the frequency of the pendulum. | A sailor notices a buoy bounce up and down 24 times over a minute. Calculate the frequency of the waves. |
| 1. State the known quantities
n = 15 t = 20s |
1. State the known quantities
n = 24 t = 60 |
| 2. Substitute the numbers into the equation and solve.
\(f = \tfrac{n}{t}\) \(f = \tfrac{15}{20}\) \(f = 0.75Hz\) |
2. Substitute the numbers into the equation and solve.
\(f = \tfrac{n}{t}\) \(f = \tfrac{24}{60}\) \(f = 0.4Hz\) |