Speed=Distance/Time

Key Stage 3

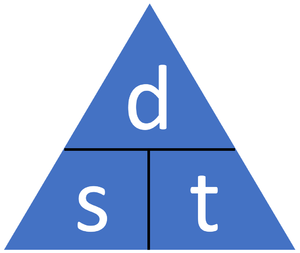
Meaning

This equation triangle shows how to rearrange the equation to find speed, distance or time. To find speed cover over the s to find it is d/t. To find distance cover over the d to find it is s x t. To find time cover over t to find it is d/s.

\[Speed = {\tfrac{distance}{time}} \] is an equation which can be used to calculate the speed of an object given the distance traveled and the time taken to travel that distance.

About Speed=Distance/Time

The standard scientific units for speed are metres per second (m/s).

The units of speed are given by the units of distance used and the units of time used in the calculation.

\[Speed = {\tfrac{distance}{time}} \] \[Speed = {\tfrac{metres}{seconds}} \] \[Speed = {\tfrac{m}{s}} \] \[Speed = m/s \]

Example Calculations

A person jogs 300metres in 120 seconds. Calculate the speed of the jogger.

distance = 300m

time = 120s

\[Speed = {\tfrac{distance}{time}} \] \[Speed = {\tfrac{300}{120}} \] \[Speed = 2.5m/s \]

A racing car travels 500metres in 10 seconds. Calculate the speed of the racing car.

distance = 500m

time = 10s

\[Speed = {\tfrac{distance}{time}} \] \[Speed = {\tfrac{500}{10}} \] \[Speed = 50m/s \]

A horse takes 20 minutes to trot 2.4 kilometres. Calculate the speed of the horse in metres per second.

distance = 2.4km = 2400m

time = 20min = 1200s

\[Speed = {\tfrac{distance}{time}} \] \[Speed = {\tfrac{2400}{1200}} \] \[Speed = 2m/s \]

The International Space Station takes 92 minutes to orbit the Earth once travelling 42,000 kilometres. Calculate the speed of the ISS.

distance = 42,000km = 42,000,000m

time = 20min = 5400s

\[Speed = {\tfrac{distance}{time}} \] \[Speed = {\tfrac{42000000}{5400}} \] \[Speed = 7608.7m/s \] \[Speed \approx 7600m/s \]