Gradient
Contents
Key Stage 3
Meaning
Gradient is how steep or shallow a line is compared to the horizontal.
About Gradient
- The gradient of a slope is how much the height increases as the horizontal distance increases. A steep slope has a large increase in height over a short horizontal distance.
- The gradient on a scatter graph is the rate at which the variable on the y-axis changes with a change on the x-axis.
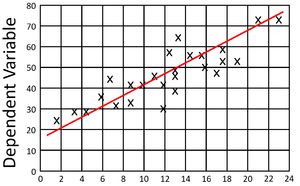
- A positive gradient on a scatter graph is one where as x increases, y increases.
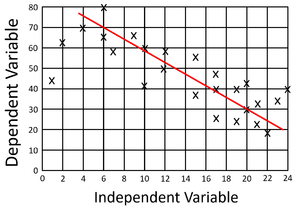
- A negative gradient on a scatter graph in one where as x increases, y decreases.
Equation
Gradient = (Change in y)/(Change in x)
\(m=\frac{y_2-y_1}{x_2-x_1}\)
Where
\(m\) = The gradient.
\(y_2\) = The final y value.
\(y_1\) = The initial y value.
\(x_2\) = The final x value.
\(x_2\) = The initial x value.
Examples
| This scatter graph shows a positive gradient. | This scatter graph shows a negative gradient. |
Key Stage 4
Meaning
Gradient is how steep or shallow a line is compared to the horizontal.
About Gradient
- The gradient of a slope is how much the height increases as the horizontal distance increases. A steep slope has a large increase in height over a short horizontal distance.
- The gradient on a scatter graph is the rate at which the variable on the y-axis changes with a change on the x-axis.
- A positive gradient on a scatter graph is one where as x increases, y increases.
- A negative gradient on a scatter graph in one where as x increases, y decreases.
Equation
Gradient = (Change in y)/(Change in x)
\(m=\frac{y_2-y_1}{x_2-x_1}\)
Where
\(m\) = The gradient.
\(y_2\) = The final y value.
\(y_1\) = The initial y value.
\(x_2\) = The final x value.
\(x_2\) = The initial x value.
| This scatter graph shows a positive gradient. | This scatter graph shows a negative gradient. |
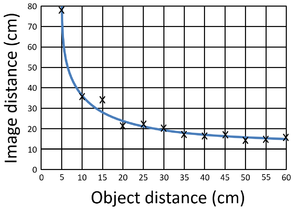
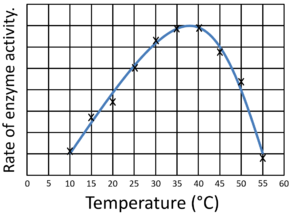
| This scatter graph of Image Distance against Object Distance of a Lens begins with a steep negative gradient which becomes more shallow until the gradient is almost zero. | This scatter graph showing how temperature affects enzyme activity begins with a steep positive gradient but then changes to a steep negative gradient. |
References
AQA
- Gradient (graph), page 370-1, GCSE Biology; Student Book, Collins, AQA
- Gradient (graph), pages 220-1, GCSE Chemistry; Student Book, Collins, AQA
- Gradient of graph, pages 145, 179, GCSE Physics; Student Book, Collins, AQA
- Gradient of graph; tangent, page 145, GCSE Physics; Student Book, Collins, AQA
- Gradients, page 303, GCSE Combined Science Trilogy; Biology, CGP, AQA
- Gradients, page 382, GCSE Biology, CGP, AQA
- Gradients, page 7, GCSE Biology; The Revision Guide, CGP, AQA
- Gradients, pages 134-135, 140, 263, GCSE Physics; Third Edition, Oxford University Press, AQA
- Gradients, pages 171-174, 246, GCSE Combined Science Trilogy; Chemistry, CGP, AQA
- Gradients, pages 203-206, 324, GCSE Chemistry, CGP, AQA
- Gradients, pages 7, 142, 210, GCSE Combined Science; The Revision Guide, CGP, AQA
- Gradients, pages 8, 71, GCSE Chemistry; The Revision Guide, CGP, AQA
Edexcel
- Gradient (of a graph), page 330, GCSE Biology, CGP, Edexcel
- Gradients of graphs, page 131, GCSE Combined Science; The Revision Guide, CGP, Edexcel
- Gradients of graphs, pages 226-229, 332, 333, GCSE Chemistry, CGP, Edexcel
- Gradients of graphs, pages 8, 80, GCSE Chemistry; The Revision Guide, CGP, Edexcel
- Gradients, page 289, GCSE Combined Science, Pearson Edexcel
- Gradients, page 5, GCSE Physics, Pearson Edexcel
- Gradients, pages 28, 346-348, GCSE Physics, CGP, Edexcel
- Gradients; tangents, page 348, GCSE Physics, CGP, Edexcel
OCR
- Gradients (graphs), page 289, Gateway GCSE Biology, Oxford, OCR
- Gradients (graphs), pages 54, 56, 288-289, Gateway GCSE Physics, Oxford, OCR
- Gradients of graphs, pages 175, 304, Gateway GCSE Chemistry, Oxford, OCR
- Gradients of graphs, pages 7, 130, 161, 162, 171, 173, Gateway GCSE Combined Science; The Revision Guide, CGP, OCR
- Gradients of graphs, pages 8, 70, Gateway GCSE Chemistry; The Revision Guide, CGP, OCR