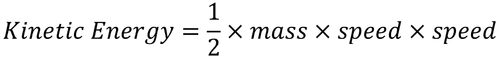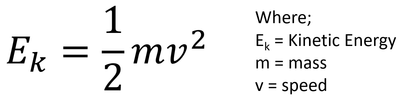Contents
Key Stage 3
Meaning

The kinetic energy store is the energy store associated with moving objects.
About The Kinetic Energy Store
- The faster an object moves the more energy it has in its kinetic store.
- If two objects are moving at the same speed the one with more mass has more energy in the kinetic store.
Equation
| The equation for kinetic energy written in words. |
| The equation for kinetic energy written in symbols. |
Calculating Kinetic Energy
| A 700kg formula one racing car has a top speed of 100m/s. Calculate the kinetic energy of the car to two significant figures. | A cheetah of mass 75kg runs at a speed of 32m/s. Calculate the kinetic energy of the cheetah correct to two significant figures. | A 160g cricket ball is hit at 44m/s. Calculate the kinetic energy of the cricket ball correct to two significant figures. |
| 1. State the known quantities
m = 700kg v = 100m/s |
1. State the known quantities
m = 75kg v = 32m/s |
1. State the known quantities
m = 160g min kilograms = \(\frac{160}{1000}\) m = 0.16kg v = 32m/s |
| 2. Substitute the numbers into the equation and solve.
\(E_k = \frac{1}{2} m v^2\) \(E_k = \frac{1}{2} \times 700 \times 100^2\) \(E_k = \frac{1}{2} \times 700 \times 10,000\) \(E_k = 3,500,000J\) |
2. Substitute the numbers into the equation and solve.
\(E_k = \frac{1}{2} m v^2\) \(E_k = \frac{1}{2} \times 75 \times 32^2\) \(E_k = \frac{1}{2} \times 75 \times 1024\) \(E_k = 38,400J\) \(E_k \approx 38000J\) |
2. Substitute the numbers into the equation and solve.
\(E_k = \frac{1}{2} m v^2\) \(E_k = \frac{1}{2} \times m \times v^2\) \(E_k = \frac{1}{2} \times 0.16 \times 44^2\) \(E_k = \frac{1}{2} \times 0.16 \times 1936\) \(E_k = 154.88J\) \(E_k \approx 150J\) |
Key Stage 4
Meaning
The kinetic energy store is the energy store associated with moving objects.
About Kinetic Energy
- Any moving object stores kinetic energy.
- The kinetic energy store of an object is related to two properties of the object:
- The mass of the object - The greater the mass the greater the kinetic energy stored.
- The speed or velocity of the object - The greater the speed the greater the kinetic energy stored.
Equation
NB: You must memorise this equation!
Kinetic Energy = 0.5 x (Mass) x (Speed)2
\(E_k = \frac{1}{2} m v^2\)
Where:
Ek = Kinetic Energy stored.
v = The speed or velocity of the object.
Calculating Kinetic Energy
| A 700kg formula one racing car has a top speed of 100m/s. Calculate the kinetic energy of the car to two significant figures. | A cheetah of mass 75kg runs at a speed of 32m/s. Calculate the kinetic energy of the cheetah correct to two significant figures. | A 160g cricket ball is hit at 44m/s. Calculate the kinetic energy of the cricket ball correct to two significant figures. |
| 1. State the known quantities
m = 700kg v = 100m/s |
1. State the known quantities
m = 75kg v = 32m/s |
1. State the known quantities
m = 160g min kilograms = \(\frac{160}{1000}\) m = 0.16kg v = 32m/s |
| 2. Substitute the numbers into the equation and solve.
\(E_k = \frac{1}{2} m v^2\) \(E_k = \frac{1}{2} \times 700 \times 100^2\) \(E_k = \frac{1}{2} \times 700 \times 10,000\) \(E_k = 3,500,000J\) |
2. Substitute the numbers into the equation and solve.
\(E_k = \frac{1}{2} m v^2\) \(E_k = \frac{1}{2} \times 75 \times 32^2\) \(E_k = \frac{1}{2} \times 75 \times 1024\) \(E_k = 38,400J\) \(E_k \approx 38000J\) |
2. Substitute the numbers into the equation and solve.
\(E_k = \frac{1}{2} m v^2\) \(E_k = \frac{1}{2} \times m \times v^2\) \(E_k = \frac{1}{2} \times 0.16 \times 44^2\) \(E_k = \frac{1}{2} \times 0.16 \times 1936\) \(E_k = 154.88J\) \(E_k \approx 150J\) |
Calculating Velocity from Kinetic Energy
| A 75kg person has a kinetic energy of 96J while while walking. Calculate their speed. | A bird of mass 2.4kg flies at a constant speed with a kinetic energy store of 1500J. Calculate the speed of the bird correct to two significant figures. | A 60g bullet has a kinetic energy store of 750J. Calculate the speed of the bullet correct to two significant figures. |
| 1. State the known quantities
Ek = 96J m = 75kg |
1. State the known quantities
Ek = 1500J m = 2.4kg |
1. State the known quantities
Ek = 750J m = 60g = 0.06kg |
| 2. Substitute the numbers and evaluate.
\(E_k = \frac{1}{2} m v^2\) \(96 = \frac{1}{2} \times 75 \times v^2\) \(96 = 37.5v^2\) |
2. Substitute the numbers and evaluate.
\(E_k = \frac{1}{2} m v^2\) \(1500 = \frac{1}{2} \times 2.4 \times v^2\) \(1500 = 1.2v^2\) |
2. Substitute the numbers and evaluate.
\(E_k = \frac{1}{2} m v^2\) \(750 = \frac{1}{2} \times 0.06 \times v^2\) \(750 = 0.03v^2\) |
| 3. Rearrange the equation and solve.
\(v^2 = \frac{96}{37.5}\) \(v = \sqrt{\frac{96}{37.5}}\) \(v = 1.6m/s\) |
3. Rearrange the equation and solve.
\(v^2 = \frac{1500}{1.2}\) \(v = \sqrt{\frac{1500}{1.2}}\) \(v = 35.35534m/s\) \(v \approx 35m/s\) |
3. Rearrange the equation and solve.
\(v^2 = \frac{750}{0.06}\) \(v = \sqrt{\frac{750}{0.06}}\) \(v = 158.1139m/s\) \(v \approx 160m/s\) |
References
AQA
- Kinetic energy stores, page 169, GCSE Combined Science; The Revision Guide, CGP, AQA
- Kinetic energy stores, pages 11, 15, GCSE Physics; The Revision Guide, CGP, AQA
- Kinetic energy stores, pages 21, 25, 27, 30, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Kinetic energy stores, pages 22, 26, 28, 31, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Kinetic energy stores; of particles, pages 34, 100, 104, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Kinetic energy stores; of particles, pages 35, 110, 114, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
Edexcel
- Kinetic energy (KE), pages 316, 323, GCSE Combined Science, Pearson Edexcel
- Kinetic energy (KE), pages 34, 41, 156, 192, GCSE Physics, Pearson Edexcel
- Kinetic energy stores, pages 61, 66, 200, GCSE Physics, CGP, Edexcel