Potential Difference
Contents
Key Stage 2
Meaning
Voltage is how much push electricity has.
About Voltage
- The bigger the voltage the more push the electricity has to go around the circuit.
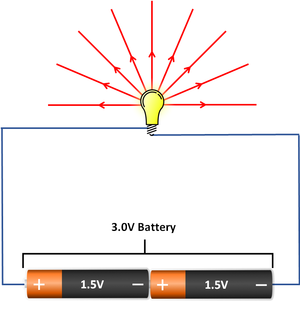
- Adding another cell to the circuit in series will increase the voltage.
- With a bigger voltage a lamp will be brighter and a buzzer will be louder.
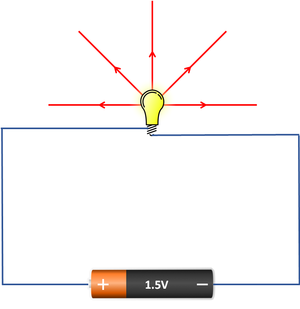
| A series circuit with one cell and one bulb. | A bulb will be brighter if the voltage is higher. |
Key Stage 3
Meaning
Potential Difference is how much energy is transferred by a current.
About Potential Difference
- Potential Difference is measured using a Voltmeter.
- The units of potential difference are Volts (V).
- Potential Difference is sometimes described as the 'push' that moves a current around a circuit.
Key Stage 4
Meaning
Potential Difference is the amount of energy transferred per unit charge between two points in a circuit.
About Potential Difference
- Potential Difference is measured using a Voltmeter.
- The units of potential difference are Volts (V).
- Potential difference is the difference in potential between two points in a circuit.
- Potential difference can be measured between two points in a circuit and is measured across a component.
- If two points in a circuit are at the same potential there is no potential difference between them so no energy is transferred between those two points.
Equation
NB: You should remember this equation with energy transferred as the subject of the formula.
Charge = (Energy Transferred)/(Potential Difference)
\(V=\frac{E}{Q}\)
Where
\(V\) = The potential difference between two points.
\(Q\) = The amount of charge that move between two points.
\(E\) = The Energy Transferred by the charge.
Example Calculations
Finding Potential Difference from Charge and Energy Transferred
| A charge of 84C transfers an energy of 20kJ. Calculate the potential difference correct to two significant figures. | 170J of energy is transferred by a charge of 92mC. Calculate the potential difference correct to two significant figures. |
| 1. State the known quantities in correct units.
Q = 84C E = 20kJ = 20x103J |
1. State the known quantities in correct units.
Q = 92mC = 92x10-3C E = 170J |
| 2. Substitute the numbers into the equation and solve.
\(V=\frac{E}{Q}\) \(V=\frac{20 \times 10^3}{84}\) \(V=238.0952V\) \(V\approx 240V\) |
2. Substitute the numbers into the equation and solve.
\(V=\frac{E}{Q}\) \(V=\frac{170}{92 \times 10^{-3}}\) \(V=1847.826V\) \(V\approx 1800V\) |
Finding Charge from Potential Difference and Energy Transferred
| The potential difference of 12V is placed across a resistor increasing its thermal energy store by 3.7J as a result. Calculate the charge that has flowed through the resistor in this time correct to two significant figures. | A circuit transfers 2.8kJ of energy electrically to a motor. The potential difference across the motor is 1.5V. Calculate thecharge that has flowed through the motor in this time correct to two significant figures. |
| 1. State the known quantities in correct units.
V = 12V E = 3.7J |
1. State the known quantities in correct units.
V = 1.5V E = 2.8kJ = 2.8x103J |
| 2. Substitute the numbers and evaluate.
\(V=\frac{E}{Q}\) \(12=\frac{3.7}{Q}\) |
2. Substitute the numbers and evaluate.
\(V=\frac{E}{Q}\) \(1.5=\frac{2.8 \times 10^3}{Q}\) |
| 3. Rearrange the equation and solve.
\(Q=\frac{3.7}{12}\) \(Q=0.3083C\) \(Q\approx0.31C\) |
3. Rearrange the equation and solve.
\(Q=\frac{2.8 \times 10^3}{1.5}\) \(Q=1866.7C\) \(Q\approx1900C\) |
Finding Energy Transferred from Charge and Potential Difference
| A bolt of lightning with a potential difference 31,000kV transfers a charge of 15C. Calculate the energy transferred by this bolt of lightning correct to two significant figures. | A 9V battery is able to mobilise a charge of 4.3kC during its operation. Calculate the total amount of energy stored in this battery correct to two significant figures. |
| 1. State the known quantities in correct units.
V = 31,000kV = 3.1x107V Q = 15C |
1. State the known quantities in correct units.
V = 9V Q = 4.3kC = 4.3x103 |
| 2. Substitute the numbers and evaluate.
\(V=\frac{E}{Q}\) \(3.1 \times 10^7=\frac{E}{15}\) |
2. Substitute the numbers and evaluate.
\(V=\frac{E}{Q}\) \(9 =\frac{E}{4.3 \times 10^3}\) |
| 3. Rearrange the equation and solve.
\(E = 15 \times 3.1 \times 10^7\) \(E = 4.65\times10^8 J\) \(E\approx4.7\times10^8 J\) |
3. Rearrange the equation and solve.
\(E = 4.3 \times 10^3 \times 9\) \(E = 38700J\) \(E \approx 39000 \times 10^4J\) |
References
AQA
- Potential difference (p.d), page 294, GCSE Combined Science Trilogy 1, Hodder, AQA
- Potential difference (p.d); current-potential difference graphs, pages 43-5, GCSE Physics, Hodder, AQA
- Potential difference (p.d); direct and alternating, page 50, GCSE Physics, Hodder, AQA
- Potential difference (p.d); in transformers, page 237, GCSE Physics, Hodder, AQA
- Potential difference (p.d); induced, pages 232-3, GCSE Physics, Hodder, AQA
- Potential difference (p.d.), page 39, GCSE Physics, Hodder, AQA
- Potential difference (p.d.); in series and parallel circuits, pages 46-7, GCSE Physics, Hodder, AQA
- Potential difference, page 185, GCSE Chemistry; Student Book, Collins, AQA
- Potential difference, pages 180, 181, GCSE Combined Science; The Revision Guide, CGP, AQA
- Potential difference, pages 24, 25, 96-98, GCSE Physics; The Revision Guide, CGP, AQA
- Potential difference, pages 52-69, 71-77, 264-5, GCSE Physics; Student Book, Collins, AQA
- Potential difference, pages 54-55, 58-61, 64-65, 67-70, 224-229, GCSE Physics; Third Edition, Oxford University Press, AQA
- Potential difference, pages 62-67, 89, 90, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Potential difference, pages 64-69, 92, 93, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Potential difference; alternating, page 188, GCSE Combined Science; The Revision Guide, CGP, AQA
- Potential difference; direct, page 188, GCSE Combined Science; The Revision Guide, CGP, AQA
- Potential difference; energy transferred, page 190, GCSE Combined Science; The Revision Guide, CGP, AQA
- Potential difference; energy transferred, page 33, GCSE Physics; The Revision Guide, CGP, AQA
- Potential difference; in parallel circuits, page 186, GCSE Combined Science; The Revision Guide, CGP, AQA
- Potential difference; in parallel circuits, page 29, GCSE Physics; The Revision Guide, CGP, AQA
- Potential difference; in parallel, pages 72, 73, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Potential difference; in parallel, pages 74, 75, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Potential difference; in series circuits, page 185, GCSE Combined Science; The Revision Guide, CGP, AQA
- Potential difference; in series circuits, page 28, GCSE Physics; The Revision Guide, CGP, AQA
- Potential difference; in series, pages 68, 69, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Potential difference; in series, pages 70, 71, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Potential difference; induced, pages 258-60, GCSE Physics; Student Book, Collins, AQA
- Potential difference; induced, pages 303-306, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Potential difference; induced, pages 96-98, GCSE Physics; The Revision Guide, CGP, AQA
- Potential difference; I-V characteristics, page 183, GCSE Combined Science; The Revision Guide, CGP, AQA
- Potential difference; I-V characteristics, page 26, GCSE Physics; The Revision Guide, CGP, AQA
- Potential difference; measuring, page 106, GCSE Physics; The Revision Guide, CGP, AQA
- Potential difference; measuring, page 239, GCSE Combined Science; The Revision Guide, CGP, AQA
- Potential difference; measuring, pages 235, 236, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Potential difference; measuring, pages 331, 332, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Potential difference; national grid, page 191, GCSE Combined Science; The Revision Guide, CGP, AQA
- Potential difference; national grid, page 34, GCSE Physics; The Revision Guide, CGP, AQA
- Potential difference; transformers, page 98, GCSE Physics; The Revision Guide, CGP, AQA
Edexcel
- Potential difference (p.d.), pages 142-143, 174, GCSE Physics, Pearson Edexcel
- Potential difference, pages 184-187, GCSE Combined Science; The Revision Guide, CGP, Edexcel
- Potential difference, pages 221, 222, GCSE Physics, CGP, Edexcel
- Potential difference, pages 71-74, GCSE Physics; The Revision Guide, CGP, Edexcel
- Potential difference; in parallel circuits, pages 235, 236, GCSE Physics, CGP, Edexcel
- Potential difference; induced, pages 280-283, GCSE Physics, CGP, Edexcel
OCR
- Potential difference (p.d.), p ages 100-101, 130-134, 136-137, Gateway GCSE Physics, Oxford, OCR
- Potential difference (p.d.); Calculations, pages 113, Gateway GCSE Physics, Oxford, OCR
- Potential difference (p.d.); Graphs, pages 106-107, Gateway GCSE Physics, Oxford, OCR
- Potential difference (p.d.); In series circuit, pages 102-103, Gateway GCSE Physics, Oxford, OCR
- Potential difference (p.d.); Measurement, pages 101, 259-260, 262, Gateway GCSE Physics, Oxford, OCR
- Potential difference, page 95, Gateway GCSE Chemistry; The Revision Guide, CGP, OCR
- Potential difference, pages 176-182, Gateway GCSE Combined Science; The Revision Guide, CGP, OCR
- Potential difference, pages 44-50, Gateway GCSE Physics; The Revision Guide, CGP, OCR