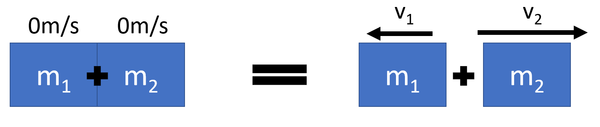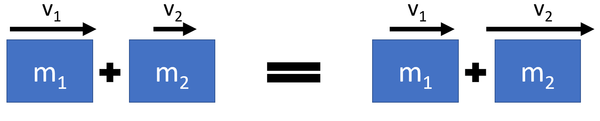Difference between revisions of "Conservation of Momentum"
(→Explosions) |
(→Elastic Collisions) |
||
| Line 152: | Line 152: | ||
<math>v_4</math> = The [[velocity]] of [[object]] 2 after the explosion. | <math>v_4</math> = The [[velocity]] of [[object]] 2 after the explosion. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |[[File:ElasticCollision.gif|center]] | ||
| + | |} | ||
====Example Elastic Collision Calculations==== | ====Example Elastic Collision Calculations==== | ||
Revision as of 14:57, 16 February 2019
Contents
Key Stage 4 Higher
Meaning
The law of conservation of momentum is the fact that the total momentum in a closed isolated system remains the same before and after an interaction.
About Conservation of Momentum
- Conservation of momentum means that if you add the momentum of every object before and event this will be the same as the total momentum after that event.
Conservation of momentum can be applied to 3 types of interaction to allow us to predict the outcome:
- Explosions - When two objects begin with zero momentum but are forced apart in opposite directions.
- Elastic Collisions - When two objects bounce off one another and the total kinetic energy before a collision is the same as the total kinetic energy after the collision.
- Inelastic Collisions - When kinetic energy is lost during a collision, often with the objects sticking together to form a larger object.
Equation
NB: You do not need to remember the equation but you must be able to apply the law of conservation of momentum.
Total Momentum Before = Total Momentum After
\(p_{before} = p_{after}\)
Where\[p_{before}\] = The total momentum before an interaction.
\(p_{after}\) = The total momentum after the interaction.
Explosions
- During an explosion a single object with zero momentum splits into two smaller objects.
- The total momentum before the explosion is zero. Due to conservation of momentum the total momentum after the explosion is also zero.
\(p_{before} = p_{after}\)
Since\[p = mv\]
Then:
\(0 = m_1 v_1 + m_2 v_2\)
Where\[m_1\] = The mass of object 1.
\(v_1\) = The velocity of object 1 after the explosion.
\(m_2\) = The mass of object 2.
\(v_2\) = The velocity of object 2 after the explosion.
Example Explosion Calculations
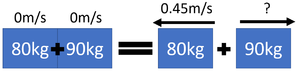
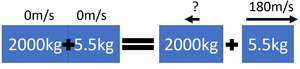
| An 80kg ice skater and a 90kg ice skater begin at rest and then push away from one another. The 80kg ice skater moves away with a velocity of 0.45m/s. Calculate the velocity of the 90kg ice skater correct to two significant figures. | An 18th century cannon of mass 2000kg fires a 5.5kg cannon ball at a velocity of 180m/s. Calculate the recoil velocity of the cannon correct to two significant figures. |
| 1. State the known quantities
pbefore = 0kgm/s m1 = 80kg m2 = 90kg v1 = 0.45m/s |
1. State the known quantities
pbefore = 0kgm/s m1 = 2000kg m2 = 5.5kg v1 = 180m/s |
| 2. Substitute the numbers and evaluate.
\(p_{before} = p_{after}\) \(0 = m_1 v_1 + m_2 v_2\) \(0 = 80 \times 0.45 + 90 \times v_2\) \(0 = 36 + 90v_2\) |
2. Substitute the numbers and evaluate.
\(p_{before} = p_{after}\) \(0 = m_1 v_1 + m_2 v_2\) \(0 = 2000 \times v_1 + 5.5 \times 180\) \(0 = 2000v_1 + 990\) |
| 3. Rearrange the equation and solve.
\(90v_2 = -36\) \(v_2 = \frac{-36}{90}\) \(v_2 = -0.40m/s\) |
3. Rearrange the equation and solve.
\(2000v_1 = -990\) \(v_1 = \frac{-990}{2000}\) \(v_1 = -0.495m/s\) \(v_1 \approx -0.50m/s\) |
Elastic Collisions
- During elastic collisions kinetic energy is conserved, so the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
- During elastic collisions the objects bounce off one another.
\(p_{before} = p_{after}\)
Since\[p = mv\]
Then:
\(m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4\)
Where\[m_1\] = The mass of object 1.
\(v_1\) = The velocity of object 1 before the explosion.
\(v_3\) = The velocity of object 1 after the explosion.
\(m_2\) = The mass of object 2.
\(v_2\) = The velocity of object 2 before the explosion.
\(v_4\) = The velocity of object 2 after the explosion.
Example Elastic Collision Calculations
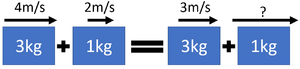
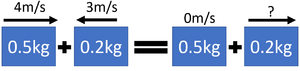
| A trolley of mass 3kg travels at a velocity of 4m/s before colliding with a trolley of mass 1kg travelling in the same direction with a velocity of 2m/s. After the collision the 3kg trolley is moving with a velocity of 3m/s. Calculate the velocity of the 1kg trolley after the collision. | A rubber ball of mass 0.5kg travels at a speed of 4m/s towards another rubber ball, of mass 0.2kg traveling in the opposite direction with a speed of 3m/s. The 0.5kg rubber ball stops completely. Calculate the velocity of the 0.2kg rubber ball after the collision. |
| 1. State the known quantities
m1 = 3kg v1 = 4m/s v3 = 3m/s m2 = 1kg v2 = 2m/s |
1. State the known quantities
m1 = 0.5kg v1 = 4m/s v3 = 0m/s m2 = 0.2kg v2 = -3m/s This is negative because it is travelling in the opposite direction. |
| 2. Substitute the numbers and evaluate.
\(m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4\) \(3 \times 4 + 1 \times 2 = 3 \times 3 + 1 \times v_4\) \(12 + 2 = 9 + v_4\) \(14 = 9 + v_4\) |
2. Substitute the numbers and evaluate.
\(m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4\) \(0.5 \times 4 + 0.2 \times (-3) = 0.5 \times 0 + 0.2 \times v_4\) \(2 -0.6 = 0 + 0.2v_4\) \(1.4 = 0.2v_4\) |
| 3. Rearrange the equation and solve.
\(v_4 = 14-9\) \(v_4 = 5m/s\) |
3. Rearrange the equation and solve.
\(v_4 = \frac{1.4}{0.2}\) \(v_4 = 7m/s\) |