Specific Latent Heat
Contents
Key Stage 4
Meaning
Specific Latent Heat is the energy required to change the state of 1kg of a substance.
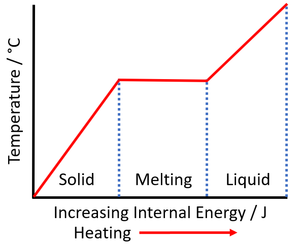
About Specific Latent Heat
- The SI Unit of specific latent heat is the J/kg.
- Different materials have a different specific latent heat.
- Specific latent heat depends on the strength of the bonds holding the particles to each other.
- The specific latent heat of a material can be found by measuring the energy needed to change the state of the material.
| The increase internal energy during the time when the temperature remains constant is the energy required to melt the material. This can be used to calculate the specific latent heat of fusion. | The increase internal energy during the time when the temperature remains constant is the energy required to vaporise the material. This can be used to calculate the specific latent heat of vaporisation. |
Equation
NB: You do not need to remember this equation but you need to be able to use it.
Specific Latent Heat = (Energy Transferred)/(Mass)
\(L = \frac{E}{m}\)
Where\[L\] = The Specific Latent Heat of the material.
\(E\) = The Energy transferred to the material during the state change.
\(m\) = The mass of the material.
Example Calculations
| An 11kg block of ice at 0°C is heated by an immersion heater until it completely melts. The immersion heater is connected to a Joulemeter which reads 3.7MJ. Calculate the specific latent heat of fusion of the water ice correct to two significant figures. | A pan containing 500g of water at 100°C is heated with an energy of 1.13kJ until all of the water has been vaporised. Calculate the specific latent heat of vaporisation of the water steam correct to two significant figures. |
| 1. State the known quantities in SI Units
E = 3.7MJ = 3.7x106J m = 11kg |
1. State the known quantities in SI Units
E = 1.13kJ = 1.13x103J m = 500g = 0.5kg |
| 2. Substitute the numbers into the equation and solve.
\(L_f = \frac{E}{m}\) \(L_f = \frac{3.7 \times 10^6}{11}\) \(L_f = 3.36363 \times 10^5 J/kg\) \(L_f \approx 3.4 \times 10^5 J/kg\) |
2. Substitute the numbers into the equation and solve.
\(L_v = \frac{E}{m}\) \(L_v = \frac{1.13 \times 10^3}{0.5}\) \(L_v = 2260 J/kg\) \(L_v \approx 2300 J/kg\) |