Contents
Key Stage 3
Meaning
Frequency is the number of waves that pass by in one second.
About Frequency
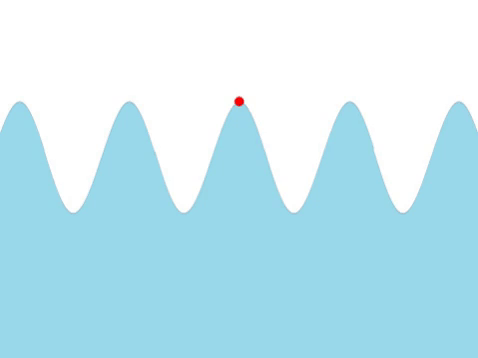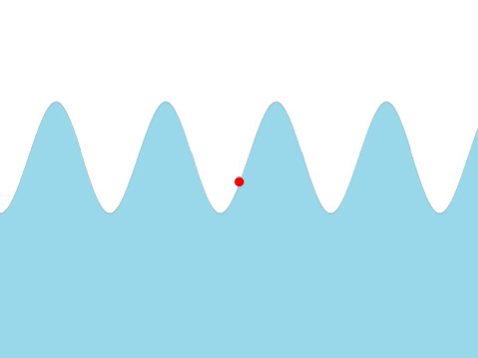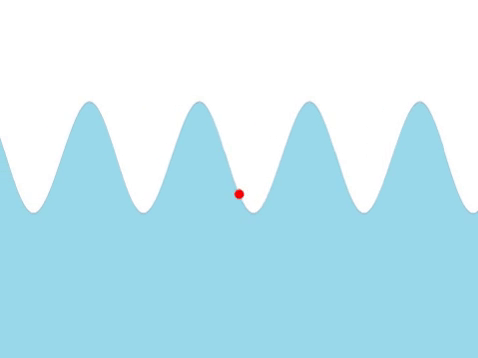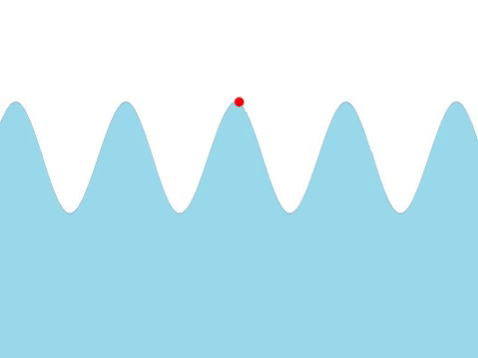
| Water Waves |
| The frequency of this wave can be found by counting the number of times the red marker oscillates every second. |
- The higher the frequency the quicker the wave oscillates.
- In sound frequency is known as pitch. A high pitch is a high frequency.
- In light frequency affects the colour of the light. Red is a low frequency and violet is a high frequency.
Equation
Frequency = 1/(Period)
\(f = \frac{1}{T}\)
Where:
f = Frequency
T = time period (the time it takes for one wave to pass a point).
Key Stage 4
Meaning
Frequency is the number of waves that pass a given point in one second.
About Frequency
- Frequency is a scalar quantity because it has magnitude but no direction.
- The SI Unit of frequency is Hertz (Hz).
| Water Waves |
| The frequency of this wave can be found by counting the number of times the red marker oscillates every second. |
- The higher the frequency the quicker the wave oscillates.
- In sound frequency is known as pitch. A high pitch is a high frequency.
- In light frequency affects the colour of the light. Red is a low frequency and violet is a high frequency.
- Frequency can be found by counting the number of waves which pass a point in a given time and dividing this by the time.
Equation
Equation 1
NB: You do not need to remember this equation but you should know how to find frequency given the time taken for one wave to pass a point.
Frequency = 1/(Period)
\(f = \frac{1}{T}\)
Where: f = Frequency
T = time period (the time it takes for a wave to pass a point).
Equation 2
NB: You do not need to remember this equation but you should know how to find frequency given the number of waves passing a point and the time taken.
Frequency = (Number of Waves which pass a point)/(Time taken for waves to pass a point)
\(f = \frac{n}{t}\)
Where: f = Frequency
n = Number of waves which pass a point.
t = The time taken for those waves to pass a point.
Equation 3
NB: You should remember this equation with v as the subject of the formula.
Frequency = (Wave Speed)/(Wavelength)
\( f = \frac{v}{\lambda}\)
Where\[ \lambda\] = The wavelength of the wave.
\(v\) = The wave speed of the wave.
\(f\) = The frequency of the wave.
Example Calculations
| A scientist wants to determine the frequency of a pendulum. They count that the pendulum oscillates 15 times over 20 seconds. Calculate the frequency of the pendulum. | A sailor notices a buoy bounce up and down 24 times over a minute. Calculate the frequency of the waves. |
| 1. State the known quantities
n = 15 t = 20s |
1. State the known quantities
n = 24 t = 60 |
| 2. Substitute the numbers into the equation and solve.
\(f = \frac{n}{t}\) \(f = \frac{15}{20}\) \(f = 0.75Hz\) |
2. Substitute the numbers into the equation and solve.
\(f = \frac{n}{t}\) \(f = \frac{24}{60}\) \(f = 0.4Hz\) |