Filtration
Contents
Key Stage 2
Meaning
Filtering is when you separate liquid from insoluble solids.
- Noun: Filtration
- Verb: To filter
- Present Participle: Filtering
- Adjective: Filtered
About Filtering
- Filtering cannot separate anything dissolved in a liquid.
- When you filter the solid will get stuck in the filter paper and the liquid will pass through.
Examples
| You can separate mud from water in the puddle with filter paper and a funnel. |
Key Stage 3
Meaning
Filtration is the process of separating a mixture of a liquid and an insoluble solid.
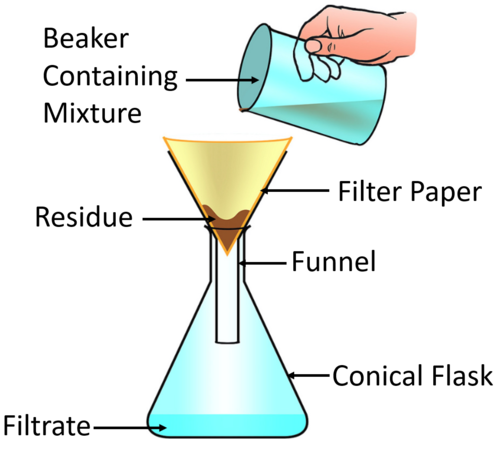
| This diagram shows how the insoluble solid gets stuck in the filter paper and is called a Residue, while the liquid passes through the filter paper into the conical flask. |
About Filtering
- Only insoluble solids can be separated by filtering.
- The solid trapped in the filter paper is called a residue.
- The liquid that has passed through the filter paper is called filtrate.
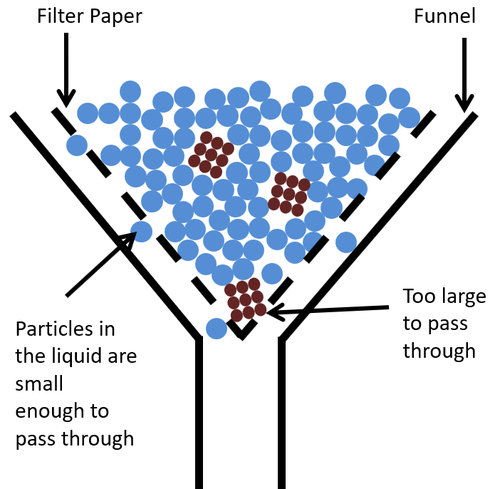
- Filtering uses a filter that has very small holes in it that allow the particles in the liquid through, but not the lumps of solid.
| This diagram shows how the insoluble solid gets stuck in the filter paper while the particles in the liquid are small enough to pass through the gaps in the filter paper. |
Key Stage 4
Meaning
Filtration is the process of removing an insoluble solid from a mixture with a liquid.
About Filtration
- In an experiment a mixture of insoluble solid and a liquid is filtered using filter paper. However, on an industrial scale many different types of filter can be used to separate insolubles solids from mixtures with liquids.
Filtration can only be used for:
- Separating a mixture of an insoluble solid and a liquid. This is done by passing the mixture through a filter.
- Separating a mixture of a soluble solid from an insoluble solid. This is done by first adding a solvent to dissolve the soluble solid before then filtering.
Filtration cannot be used for:
- Separating two solutes from each other in solution - Chromatography
- Separating solutes from solvents in solution - Distillation
- Separating two solvents from each other in solution - Fractional Distillation
References
AQA
- Filtrate, pages 200-201, GCSE Biology; Student Book, Collins, AQA
- Filtrates/filtration, page 8, GCSE Chemistry; Third Edition, Oxford University Press, AQA
- Filtration (in kidneys), page 215, GCSE Biology, CGP, AQA
- Filtration (Kidneys), page 75, GCSE Biology; The Revision Guide, CGP, AQA
- Filtration, page 17, GCSE Chemistry; The Revision Guide, CGP, AQA
- Filtration, page 23, GCSE Chemistry, Hodder, AQA
- Filtration, page 37, GCSE Chemistry, CGP, AQA
- Filtration, page 37, GCSE Combined Science Trilogy; Chemistry, CGP, AQA
- Filtration, pages 137, 138, GCSE Combined Science Trilogy 1, Hodder, AQA
- Filtration, pages 18, 144, 146-7, 263-4, 322, GCSE Chemistry; Student Book, Collins, AQA
Edexcel
- Filtration, page 158, GCSE Biology, Pearson, Edexcel
- Filtration, pages 101, 104, GCSE Combined Science; The Revision Guide, CGP, Edexcel
- Filtration, pages 104, 112, GCSE Chemistry, CGP, Edexcel
- Filtration, pages 150, 201, GCSE Combined Science, Pearson Edexcel
- Filtration, pages 38, 41, GCSE Chemistry; The Revision Guide, CGP, Edexcel
- Filtration, pages 6, 57, GCSE Chemistry, Pearson, Edexcel
- Filtration; laboratory practice, page 151, GCSE Combined Science, Pearson Edexcel
- Filtration; laboratory practice, page 7, GCSE Chemistry, Pearson, Edexcel