Resultant Force
Contents
Key Stage 3
Meaning
The Resultant Force is the overall force on an object.
About Resultant Forces
- A resultant force can be calculated by taking forces that act along the same line and add them together.
- If the forces are in the same direction as each other, then they have a positive value.
- If one force is acting in the opposite direction to another one of the forces is given a negative value.
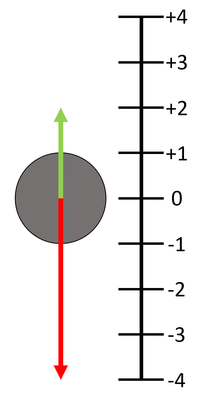
| If the 'up' direction is chosen to be positive then any vector pointing 'up' has a positive value and any vector pointing 'down' has a negative value.
In this diagram the green vector has a value of +2 while the red vector has a value of -4. If the number lines represent the number of Newtons force then the Resultant Force is the two values added together. FR = (+2N) + (-4N) FR = -2N upwards |
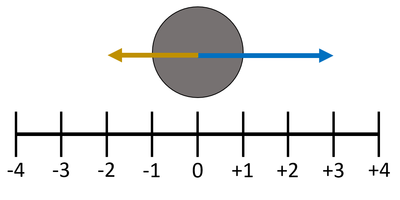
| If the 'right' direction is chosen to be positive then any vector pointing 'right' has a positive value and any vector pointing 'left' has a negative value.
In this diagram the blue vector has a value of +3 while the yellow vector has a value of -2. If the number lines represent the number of Newtons force then the Resultant Force is the two values added together. FR = (+3N) + (-2N) FR = 1N to the right |
Examples
|
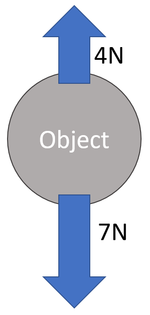
Choose which directions are positive. Up is positive. Calculate the Resultant Force. FR = (+4N) + (-7N) FR = -3N up |
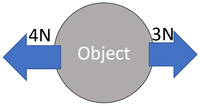
Choose which directions are positive. Right is positive. Calculate the Resultant Force. There is 4N left and 3N right. FR = (+3N) + (-4N) FR = -1N right |
Choose which directions are positive. Up is positive. Right is positive. Calculate the Resultant Force. FVertical = (+6N) + (-6N) FVertical = 0N up There is 6N left and 4N right. FHorizontal = (+4N) + (-6N) FHorizontal = -2N right |
Key Stage 4
Meaning
The resultant force is the sum of all forces acting on an object.
About Resultant Forces
- When forces act in the same direction their magnitudes are added together.
- When forces act along the same line but in opposite directions; one is subtracted from the other.
- When forces are at right angles to one another they can be added using Pythagoras' Theorem to find the magnitude of the resultant force and then trigonometry can be used to find the direction of the resultant force.
Examples
|
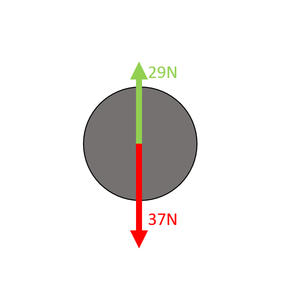
Choose which directions are positive. Up is positive. Calculate the Resultant Force There is 29N up and 37N down. FR = (+29N) + (-37N) FR = -8N upwards |
|
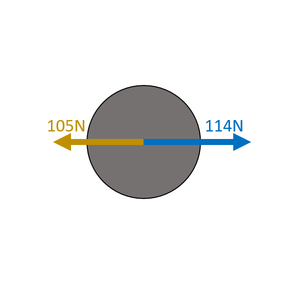
Choose which directions are positive. Right is positive. Calculate the Resultant Force There is 114N right and 105N left. FR = (+114N) + (-105N) FR = 9N right |
|
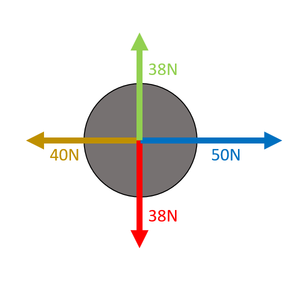
Choose which directions are positive. Right is positive. Up is positive. Calculate the Resultant Force There is 38N up and 38N down. FR = (+38N) + (-38N) FR = 0N upwards Calculate the Resultant Force There is 50N right and 40N left. FR = (+50N) + (-40N) FR = 10N right |
|
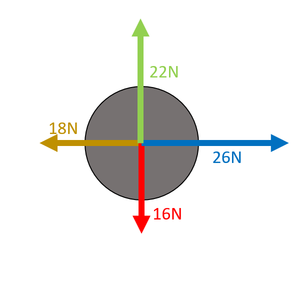
Choose which directions are positive. Right is positive. Up is positive. Calculate the Resultant Force There is 22N up and 16N down. FVertical = (+22N) + (-16N) FVertical = 6N upwards Calculate the Resultant Force There is 26N right and 18N left. FHorizontal = (+26N) + (-18N) FHorizontal = 8N right Since there are two resultant forces that are perpendicular they form a right angle triangle and their hypotenuse is the magnitude of the resultant force. This can be found using Pythagoras' Theorem. \({F_R}^2 = {F_V}^2 + {F_H}^2\) \(F_R = \sqrt{6^2 + 8^2}\) \(F_R = \sqrt{100}\) \(F_R = 10N\) The angle from the horizontal can be found using Trigonometry. \(\tan \theta = \frac{Opposite}{Adjacent}\) \(\tan \theta = \frac{6}{8}\) \(\theta = 36.9^\circ \) up from horizontal |
References
AQA
- Resultant force, pages 155-8, GCSE Physics; Student Book, Collins, AQA
- Resultant force, pages 205, 212, GCSE Combined Science; The Revision Guide, CGP, AQA
- Resultant force, pages 53, 54, 64, 71, GCSE Physics; The Revision Guide, CGP, AQA
- Resultant forces, page 131, 132, 162-165, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Resultant forces, pages 118-119, 144-145, 148-149, 168-169, GCSE Physics; Third Edition, Oxford University Press, AQA
- Resultant forces, pages 120-1, GCSE Physics, Hodder, AQA
- Resultant forces, pages 151, 152, 194-197, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Resultant forces, pages 210-11, GCSE Combined Science Trilogy 2, Hodder, AQA
Edexcel
- Resultant forces, page 209, GCSE Physics, CGP, Edexcel
- Resultant forces, pages 12-13, 134, GCSE Physics, Pearson Edexcel
- Resultant forces, pages 181, 182, GCSE Combined Science; The Revision Guide, CGP, Edexcel
- Resultant forces, pages 67, 68, GCSE Physics; The Revision Guide, CGP, Edexcel