Vector
Contents
Key Stage 4
Meaning
A vector is a quantity with both magnitude and direction.
About Vectors
Vector quantities include:
- Forces \(\overrightarrow{F}\) - A push or a pull which has a magnitude (size) and a direction.
- Displacement \(\overrightarrow{s}\) - The distance and direction from one point in space to another.
- Velocity \(\overrightarrow{v}\) - The speed and direction that an object is moving.
- Acceleration \(\overrightarrow{a}\) - The rate of change of velocity and the direction of this change.
If a quantity does not include direction, then it is called a scalar, not a vector.
Representing Vectors
- Vectors are written with either an underline (\(\underline{F}\),\(\underline{s}\),\(\underline{v}\),\(\underline{a}\)) or an arrow above (\(\overrightarrow{F}\),\(\overrightarrow{s}\),\(\overrightarrow{v}\),\(\overrightarrow{a}\)).
- Vectors are often drawn on diagrams. They are drawn as an arrow because an arrow can show the magnitude (the length of the arrow) and the direction (which way the arrow is pointing).
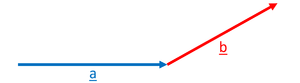
| The vector \(\underline{a}\) is shown by this arrow. The length of the arrow represents the magnitude of the vector and the direction of the arrow shows the direction of the vector. | The vector \(\underline{b}\) is shown by this arrow. The length of the arrow represents the magnitude of the vector and the direction of the arrow shows the direction of the vector. |
| The arrow \(\underline{b}\) is shorter than the arrow \(\underline{a}\) so the vector \(\underline{b}\) has a smaller magnitude than \(\underline{a}\). It can also be seen that vector \(\underline{b}\) has a different direction to vector \(\underline{a}\). | |
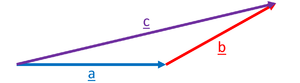
| The two vectors can be added by placing the start of one vector at the end of the other. | A new vector \(\underline{c}\) is created from the addition of \(\underline{a}\) and \(\underline{b}\).
\(\underline{a}+\underline{b}=\underline{c}\) |
| If the vectors are drawn accurately in length using a ruler and in direction using a protractor the length and direction of the new vector can be measured from the diagram. This type of Scale Diagram can be used to find the magnitude and direction of the new vector without calculation. | |
References
AQA
- Vector, pages 143, 157, 162-3, GCSE Physics; Student Book, Collins, AQA
- Vector; diagram, page 157, GCSE Physics; Student Book, Collins, AQA
- Vectors, pages 114-115, 130-131, GCSE Physics; Third Edition, Oxford University Press, AQA
- Vectors, pages 117, 148, GCSE Physics, Hodder, AQA
- Vectors, pages 127, 147, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Vectors, pages 147, 148, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Vectors, pages 207, 226, GCSE Combined Science Trilogy 2, Hodder, AQA
- Vectors, pages 42, 203, GCSE Combined Science; The Revision Guide, CGP, AQA
- Vectors, pages 51, 54, 60, GCSE Physics; The Revision Guide, CGP, AQA
- Vectors, pages 83, 224-225, GCSE Biology; Third Edition, Oxford University Press, AQA
- Vectors, pages, 46, 48, 99, GCSE Biology; The Revision Guide, CGP, AQA
- Vectors; Drawing them, pages 208, GCSE Combined Science Trilogy 2, Hodder, AQA
- Vectors; in genetic engineering, page 240, GCSE Combined Science Trilogy; Biology, CGP, AQA
- Vectors; in genetic engineering, page 294, GCSE Biology, CGP, AQA
- Vectors; momentum as, page 170, GCSE Physics, Hodder, AQA
- Vectors; Momentum as, pages 245, 246, GCSE Combined Science Trilogy 2, Hodder, AQA
- Vectors; of disease pages 130, 133 ,135, GCSE Biology, CGP, AQA
- Vectors; of disease, pages 124, 127, 129, GCSE Combined Science Trilogy; Biology, CGP, AQA
- Vectors; representation by arrows, page 119, GCSE Physics, Hodder, AQA
Edexcel
- Vectors (biology), pages 37, 39, GCSE Combined Science; The Revision Guide, CGP, Edexcel
- Vectors (disease transfer), page 105, GCSE Biology, Pearson, Edexcel
- Vectors (genetic), page 89, GCSE Biology, Pearson, Edexcel
- Vectors, page 12, GCSE Physics; The Revision Guide, CGP, Edexcel
- Vectors, pages 22, 205, GCSE Physics, CGP, Edexcel
- Vectors, pages 2-3, 132, GCSE Physics, Pearson Edexcel
- Vectors, pages 3, 12, 121, GCSE Physics, Pearson Edexcel
- Vectors; in disease, page 55, GCSE Biology; The Revision Guide, CGP, Edexcel
- Vectors; in disease, pages 154, 156, GCSE Biology, CGP, Edexcel
- Vectors; in genetic engineering, page 52, GCSE Biology; The Revision Guide, CGP, Edexcel
- Vectors; in genetic engineering, pages 144, 155, GCSE Biology, CGP, Edexcel
- Vectors; viruses, page 195, GCSE Biology, Pearson, Edexcel
OCR
- Vector quantities, page 157, Gateway GCSE Combined Science; The Revision Guide, CGP, OCR
- Vectors (genetic engineering), page 204, Gateway GCSE Biology, Oxford, OCR
- Vectors, pages 50-51, 65, Gateway GCSE Physics, Oxford, OCR