Acceleration
Contents
Key Stage 3
Meaning
Acceleration is an increase in speed.
About Acceleration
- The opposite of acceleration is deceleration which is to slow down.
- Acceleration happens when an object experiences Unbalanced Forces.
Acceleration Equation
\(a = {\frac{v-u}{t}} \)
Where:
- a = acceleration
- v = final speed
- u = initial speed
- t = time
Example Calculations
| A person starts at rest and accelerates to a speed of 8m/s in 0.8 seconds. Calculate the acceleration of the person. | A racing car travels comes around a corner at a speed of 20m/s and in 1.5 seconds accelerates to a speed of 80m/s. Calculate the acceleration of the racing car. |
|
final speed = 8m/s initial speed = 0m/s time = 0.8s \(a = {\frac{v-u}{t}} \) \(a = {\frac{8-0}{0.8}} \) \(a = {\frac{8}{0.8}} \) \(a = 10m/s/s \) |
final speed = 80m/s initial speed = 20m/s time = 1.5s \(a = {\frac{v-u}{t}} \) \(a = {\frac{80-20}{1.5}} \) \(a = {\frac{60}{1.5}} \) \(a = 40m/s/s \) |
| A horse begins trotting at 3.0m/s and accelerates to canter at 11m/s in 2.0 seconds. Calculate the acceleration of the horse. | A space probe is travelling at 18,000m/s and uses a thruster for 250 seconds to slow down to 6,000m/s. Calculate the acceleration of the space probe. |
|
final speed = 11m/s initial speed = 3.0m/s time = 2.0s \(a = {\frac{v-u}{t}} \) \(a = {\frac{11-3.0}{2.0}} \) \(a = {\frac{8.0}{2.0}} \) \(a = 4m/s/s \) |
final speed = 18,000m/s initial speed = 6,000m/s time = 250s \(a = {\frac{v-u}{t}} \) \(a = {\frac{6,000-18,000}{250}} \) \(a = {\frac{-12,000}{250}} \) \(a = -48m/s/s \) |
Key Stage 4
Meaning
Acceleration is a vector quantity that describes the rate of change of velocity.
About Acceleration
- Acceleration is a vector because it has a magnitude and direction.
- The SI Units of acceleration and metres per second per second (m/s/s).
Acceleration may refer to:
- Increasing speed - The magnitude of the velocity increases.
- Decreasing speed - The magnitude of the velocity decreases, also known as deceleration.
- Changing direction - The magnitude of the velocity remains constant (constant speed) but the object changes direction of travel.
- Newton's First Law indicates that acceleration occurs due to unbalanced forces on an object:
An object in motion will tend to stay in motion in a straight line and an object at rest will tend to stay at rest unless an unbalanced force acts upon it.
Force and Acceleration
- Newton's Second Law indicates that acceleration of an object is directly proportional to the resultant force on the object but inversely proportional to its mass.
Typical Accelerations
You should be able to estimate the acceleration for these events:
| Event | Acceleration in m/s/s |
| A falling object | 9.8 |
| Start running | 3.0 |
| Car accelerating | 4.0 |
| Passenger Jet Takeoff | 5.0 |
| Fighter Jet Takeoff | 60 |
Examples
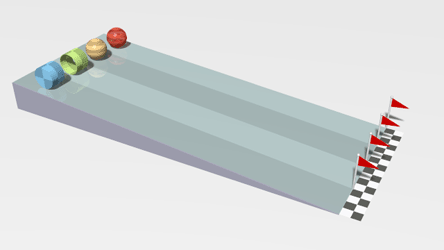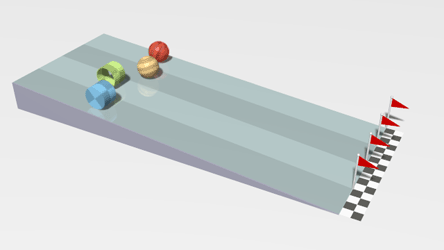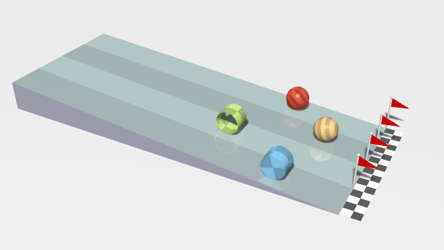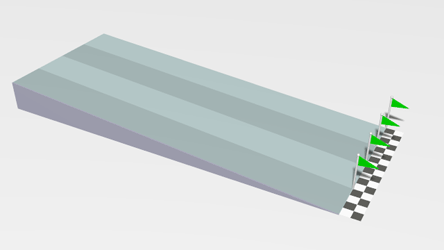
| This animation shows a linear acceleration as the objects roll down the slope. | This animation shows acceleration due to a changing direction. |
| In this animation there is linear acceleration and deceleration as the cars change speed as well as an acceleration due to changing direction.
The passengers notice this acceleration because it feels as if a force is acting on them:
|
Equations
Acceleration, Velocity and Time
NB: You must remember this equation.
This equation applies to linear acceleration but not to a change in direction.
acceleration = (Change in Velocity)/(Time)
\(a = {\frac{\Delta v}{t}} \)
Where
\(a\) = Acceleration of the object.
\(\Delta v\) = Change in magnitude of the velocity: The difference between Final Velocity (v) and Initial Velocity (u) (v-u)
\(t\)= Time taken for the change in velocity.
Acceleration, Mass and Force
NB: You must remember this equation.
\(a = {\frac{F}{m}} \)
Where:
Force = Mass x Acceleration
\(F=ma\)
Where
\(F\) = The Resultant Force on the object.
\(m\) = The mass of the object.
\(a\) = The acceleration of the object.
Example Calculations
Finding Acceleration given Change in Velocity and Time
| A person starts at rest and accelerates to a speed of 7.8m/s in 0.64 seconds. Calculate the acceleration of the person correct to two significant figures. | A racing car travels comes around a corner at a speed of 25m/s and in 1.4 seconds accelerates to a speed of 73m/s. Calculate the acceleration of the racing car correct to two significant figures. |
| 1. State the known quantities
\(\Delta v\) = 7.8 - 0 = 7.8m/s time = 0.64s |
1. State the known quantities
\(\Delta v\) = 73 - 25 = 48m/s time = 1.5s |
| 2. Substitute the numbers into the equation and solve.
\(a = {\frac{\Delta v}{t}} \) \(a = {\frac{7.8}{0.64}} \) \(a = 12.1875m/s/s \) \(a \approx 12m/s/s\) |
2. Substitute the numbers into the equation and solve.
\(a = {\frac{\Delta v}{t}} \) \(a = {\frac{48}{1.5}} \) \(a = 32m/s/s \) |
| A horse begins trotting at 3.2m/s and accelerates to canter at 11m/s in 1.8 seconds. Calculate the acceleration of the horse correct to two significant figures. | A space probe is travelling at 18,100m/s and uses a thruster for 4.25 minutes to slow down to 6,200m/s. Calculate the acceleration of the space probe correct to two significant figures. |
| 1. State the known quantities
\(\Delta v\) = 11 - 3.2 = 7.8m/s time = 1.8s |
1. State the known quantities
\(\Delta v\) = 6,200 - 18,100 = -11900m/s time = 4.25min = 255s |
| 2. Substitute the numbers into the equation and solve.
\(a = {\frac{\Delta v}{t}} \) \(a = {\frac{7.8}{1.8}} \) \(a = 4.333m/s/s \) \(a \approx 4.3m/s/s\) |
2. Substitute the numbers into the equation and solve.
\(a = {\frac{\Delta v}{t}} \) \(a = {\frac{-11900}{255}} \) \(a = -46.67m/s/s \) \(a \approx -47m/s/s\) |
Finding the Acceleration given Mass and Force
| A 7kg object is subjected to a resultant force of 53N. Calculate the acceleration of the object correct to two significant figures. | A 160g snooker ball experiences a resultant force of 12N. Calculate the acceleration of the snooker ball correct to two significant figures. |
| 1. State the known quantities
m = 7kg F = 53N |
1. State the known quantities
m = 160g = 0.16kg F = 12N |
| 2. Substitute the numbers and evaluate.
\(F=ma\) \(53=7a\) |
2. Substitute the numbers and evaluate.
\(F=ma\) \(12=0.16a\) |
| 3. Rearrange the equation and solve.
\(a = \frac{53}{7}\) \(a = 7.571m/s/s\) \(a \approx 7.6m/s/s\) |
3. Rearrange the equation and solve.
\(a = \frac{12}{0.16}\) \(a = 75m/s/s\) |
Finding Change in Velocity given Acceleration and Time
| A car begins from rest and accelerates at a rate of 4.5m/s/s for 23 seconds. Calculate the change in velocity of the car correct to two significant figures. | A person on The Moon drops a ball vertically. The acceleration due to gravity on The Moon is 1.6m/s/s. Calculate the change in velocity of the ball after 5.3seconds, correct to two significant figures. |
| 1. State the known quantities
a = 4.5m/s/s t = 23s |
1. State the known quantities
a = 1.6m/s/s t = 5.3s |
| 2. Substitute the numbers and evaluate.
\(a = {\frac{\Delta v}{t}} \) \(4.5 = {\frac{\Delta v}{23}} \) |
2. Substitute the numbers and evaluate.
\(a = {\frac{\Delta v}{t}} \) \(1.6 = {\frac{\Delta v}{5.3}} \) |
| 3. Rearrange the equation and solve.
\(\Delta v = 4.5 \times 23\) \(\Delta v = 103.5m/s\) \(\Delta v \approx 100m/s\) |
3. Rearrange the equation and solve.
\(\Delta v = 1.6 \times 5.3\) \(\Delta v = 8.48m/s\) \(\Delta v \approx 8.5m/s\) |
Finding Time Taken given Acceleration and Change in Velocity
| A ferry travelling at 5m/s slows down for a harbor at a rate of 0.02m/s/s. Calculate the time taken for the ferry to decelerate to 0.1m/s, correct to two significant figures. | A charged particle is accelerated from rest at a rate of 1300m/s/s in an electric field. Calculate the time taken to accelerated to 1,500,000m/s correct to two significant figures. |
| 1. State the known quantities
\(\Delta v\) = 0.1 - 5 = -4.9m/s a = -0.02m/s/s |
1. State the known quantities
\(\Delta v\) = 1,500,000 - 0 = 1,500,000m/s a = 1300m/s/s |
| 2. Substitute the numbers and evaluate.
\(a = {\frac{\Delta v}{t}} \) \(-0.02 = {\frac{-4.9}{t}} \) |
2. Substitute the numbers and evaluate.
\(a = {\frac{\Delta v}{t}} \) \(1300 = {\frac{1500000}{t}} \) |
| 3. Rearrange the equation and solve.
\(-0.002 = {\frac{-4.9}{t}} \) \(-0.002t = -4.9\) \(t = {\frac{-4.9}{-0.02}} \) \(t = 245s\) \(t \approx 250s\) |
3. Rearrange the equation and solve.
\(1300 = {\frac{1500000}{t}} \) \(1300t = 1500000\) \(t = {\frac{1500000}{1300}} \) \(t = 1153.85s \) \(t \approx 1200s\) |
References
AQA
- Acceleration, pages 136-138, 140-141, 144-147, GCSE Physics; Third Edition, Oxford University Press, AQA
- Acceleration, pages 140-1, 145-51, 158-61, GCSE Physics; Student Book, Collins, AQA
- Acceleration, pages 150, 151, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Acceleration, pages 152-3, GCSE Physics, Hodder, AQA
- Acceleration, pages 181, 182, 196, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Acceleration, pages 209, 212, 214, GCSE Combined Science; The Revision Guide, CGP, AQA
- Acceleration, pages 228, 230, GCSE Combined Science Trilogy 2, Hodder, AQA
- Acceleration, pages 61, 64, 66, GCSE Physics; The Revision Guide, CGP, AQA
- Acceleration; Calculation from velocity-time'
- Acceleration; definition, page 146, GCSE Physics; Student Book, Collins, AQA
- Acceleration; due to gravity, page 151, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Acceleration; due to gravity, page 182, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Acceleration; due to gravity, pages 146, 291, GCSE Physics; Student Book, Collins, AQA
- Acceleration; estimating, page 209, GCSE Combined Science; The Revision Guide, CGP, AQA
- Acceleration; Graphs, pages 230-1, GCSE Combined Science Trilogy 2, Hodder, AQA
- Acceleration; investigating, pages 160-3, GCSE Physics; Student Book, Collins, AQA
- Acceleration; investigating, pages 167, 168, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Acceleration; investigating, pages 199, 200, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Acceleration; investigation of relationship to force, pages 160-1, GCSE Physics, Hodder, AQA
- Acceleration; Investigation of, pages 238-9, GCSE Combined Science Trilogy 2, Hodder, AQA
- Acceleration; Newton`s second law of motion, pages 236-7, GCSE Combined Science Trilogy 2, Hodder, AQA
- Acceleration; Newton’s second law of motion, pages 158-9, GCSE Physics, Hodder, AQA
- Acceleration; on distance-time graphs, page 152, 153, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Acceleration; on distance-time graphs, pages 183, 184, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Acceleration; on velocity-time graphs, page 155, 156, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Acceleration; on velocity-time graphs, pages 186, 187, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Acceleration; orbits, page 101, GCSE Physics; The Revision Guide, CGP, AQA
Edexcel
- Acceleration, page 25, GCSE Physics, CGP, Edexcel
- Acceleration, pages 13, 15, 16, 106, GCSE Physics; The Revision Guide, CGP, Edexcel
- Acceleration, pages 146, 148, 149, 210, GCSE Combined Science; The Revision Guide, CGP, Edexcel
- Acceleration, pages 287, 290-291, 296, 308, GCSE Combined Science, Pearson Edexcel
- Acceleration, pages 3, 6-7, 12, 24, GCSE Physics, Pearson Edexcel
- Acceleration; dangers, page 53, GCSE Physics, CGP, Edexcel
- Acceleration; distance/time graphs, page 27, GCSE Physics, CGP, Edexcel
- Acceleration; due to gravity, page 26, GCSE Physics, CGP, Edexcel
- Acceleration; Newton’s Second Law, page 35, GCSE Physics, CGP, Edexcel
- Acceleration; uniform, page 26, GCSE Physics, CGP, Edexcel
- Acceleration; velocity/time graphs, page 31, GCSE Physics, CGP, Edexcel
OCR
- Acceleration, pages 159-162, Gateway GCSE Combined Science; The Revision Guide, CGP, OCR
- Acceleration, pages 22-25, 28, 29, 89, Gateway GCSE Physics; The Revision Guide, CGP, OCR
- Acceleration, pages 51-52, 217, 222-223, 254-254, Gateway GCSE Physics, Oxford, OCR
- Acceleration; calculations, pages 52-53, 56-57, 69, 255, Gateway GCSE Physics, Oxford, OCR
- Acceleration; due to gravity, page 83, Gateway GCSE Physics, Oxford, OCR
Key Stage 5
Meaning
Acceleration is the rate of change of velocity per unit time.
About Acceleration
- It can be positive (speeding up) or negative (slowing down), also called deceleration.
- Measured metres per second squared (m/s²).
- Acceleration be caused by changes in speed or direction.
- Newton's Second Law states that acceleration is produced when a force acts on a mass (F = ma).
- Acceleration can be uniform or non-uniform.
- The direction of the acceleration vector determines the direction of the change in velocity.
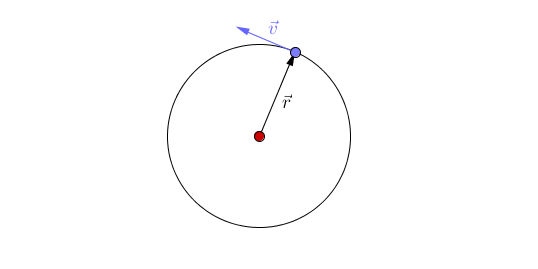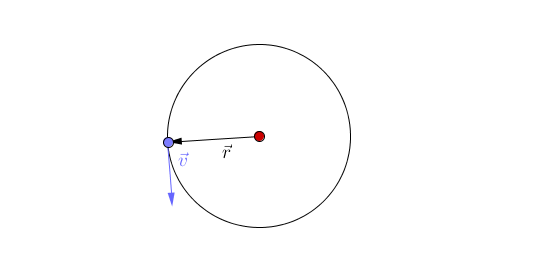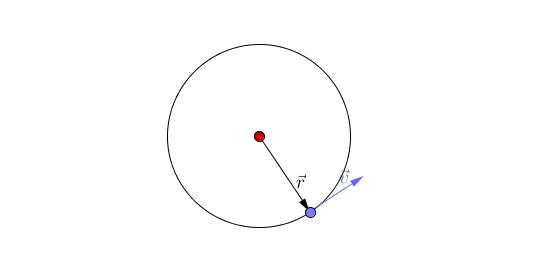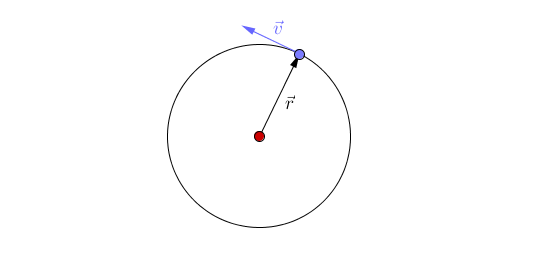
- Centripetal acceleration occurs when an object moves in a circular path and is directed towards the centre of the circle.
- Gravitational acceleration near the Earth’s surface is approximately 9.8 m/s².
Examples
- A car accelerating from a stoplight.
- The acceleration due to gravity is 9.8 m/s² downwards.