Difference between revisions of "Half Life"

Revision as of 12:15, 9 March 2019

Key Stage 4

Meaning

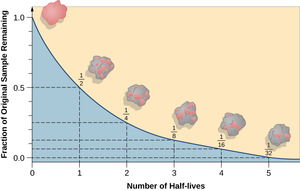
A graph showing the fraction of unstable isotope left compared to the half life.

A half life is the time it takes for half of the unstable isotopes in a radioactive sample to decay.

About Half Life

Every isotope has a unique half life.

The half life of an isotope depends on how stable the isotope is.

The half life of an isotope can be determined by measuring the emission of ionising radiation. The time it takes for the count rate of ionising radiation to halve, is the same as its half life.


This diagram shows the number of Fermium-252 atoms halves each day, so the half life is 1 day.

The half life of an isotope can be found from plotting a graph of the amount or isotope or the count rate against the time. The half life is the time these take to halve from their initial value.

The count rate of a sample of unstable isotope can be predicted given its initial count rate, its half life and the time it has been given.

Finding Half Life and Count Rate

Time /s	0	10	20	30	40	50	60	70	80
Count rate /Bq	1000	707	500	353	250	176	125	88	62

1. Find the half life of this sample of radioactive isotope.

The half life of of this sample of radioactive isotope can be found by halving the initial count rate.

1000/2 = 500Bq

The isotope took 20 seconds to half in count rate:

Half life = 20 seconds.

2. Predict the count rate at 90 seconds.

Since the half life is 20 seconds the count rate 20 seconds earlier can be halved. :At 70 seconds the count rate was 88Bq. Therefore at 90 seconds the count rate would be:

88/2 = 44Bq

3. Predict what the count rate was 10 seconds before the sample was first tested.

Since the half life is 20 seconds the count rate 20 seconds later can be doubled. :At 10 seconds the count rate was 707Bq. Therefore at -10 seconds the count rate would have been:

707x2= 1414Bq

Time /min	0	1	2	3	4	5	6	7	8
Count rate /Bq	5000	3968	3150	2500	1984	1575	1250	992	788

@@ Line 44: / Line 44: @@
 |}
-The '''half life''' of of this [[sample]] of [[radioactive]] [[isotope]] can be found by halving the initial count rate.
+. Find the '''half life''' of this [[sample]] of [[radioactive]] [[isotope]].
+:The '''half life''' of of this [[sample]] of [[radioactive]] [[isotope]] can be found by halving the initial count rate.
-/2 = 500Bq
+:1000/2 = 500Bq
-The [[isotope]] took 20 seconds to half in [[Count Rate|count rate]] so the '''half life''' is 20 [[seconds]].
+:The [[isotope]] took 20 seconds to half in [[Count Rate|count rate]]:
+:'''Half life''' = 20 [[seconds]].
-The [[Count Rate|count rate]] at 90 seconds can be predicted. Since the '''half life''' is 20 seconds the [[Count Rate|count rate]] 20 seconds earlier can be halved. At 70 seconds the [[Count Rate|count rate]] was 88Bq. Therefore at 90 seconds the [[Count Rate|count rate]] would be:
+. Predict the [[Count Rate|count rate]] at 90 seconds.
+:Since the '''half life''' is 20 seconds the [[Count Rate|count rate]] 20 seconds earlier can be halved. :At 70 seconds the [[Count Rate|count rate]] was 88Bq. Therefore at 90 seconds the [[Count Rate|count rate]] would be:
-/2 = 44Bq
+:88/2 = 44Bq
-The [[Count Rate|count rate]] at 10 seconds before the sample was first tested can also be predicted. Since the '''half life''' is 20 seconds the [[Count Rate|count rate]] 20 seconds later can be doubled. At 10 seconds the [[Count Rate|count rate]] was 707Bq. Therefore at -10 seconds the [[Count Rate|count rate]] would have been:
+. Predict what the [[Count Rate|count rate]] was 10 seconds before the [[sample]] was first tested.
+:Since the '''half life''' is 20 seconds the [[Count Rate|count rate]] 20 seconds later can be doubled. :At 10 seconds the [[Count Rate|count rate]] was 707Bq. Therefore at -10 seconds the [[Count Rate|count rate]] would have been:
-x2= 1414Bq
+:707x2= 1414Bq
 {| class="wikitable"