Difference between revisions of "Hooke's Law"
(→About Hooke's Law) |
(→Meaning) |
||
| (13 intermediate revisions by 2 users not shown) | |||
| Line 4: | Line 4: | ||
===About Hooke's Law=== | ===About Hooke's Law=== | ||
| − | : '''Hooke's Law''' describes how [[elastic]] [[object]]s behave when a pair of opposing [[force]]s | + | : '''Hooke's Law''' describes how [[elastic]] [[object]]s behave when a pair of opposing [[force]]s, one at each end of the [[object]], are applied. |
| − | : '''Hooke's Law''' is described by the equation: Force = Spring Constant x Extension | + | : '''Hooke's Law''' is described by the equation: Force = (Spring Constant) x (Extension) |
{| class="wikitable" | {| class="wikitable" | ||
| Line 16: | Line 16: | ||
===Equation=== | ===Equation=== | ||
| + | |||
| + | Force = (Spring Constant) x (Extension of the spring) | ||
| + | |||
| + | <math> F = kx </math> | ||
| + | |||
| + | <math> F = k \times x </math> | ||
| + | |||
| + | Where | ||
| + | |||
| + | <math>F</math> = [[Force]] applied | ||
| + | |||
| + | <math>k</math> = [[Spring Constant]] (stiffness of the elastic object) | ||
| + | |||
| + | <math>x</math> = [[Extension]] of the [[object]] | ||
| + | |||
| + | ===Example Calculations=== | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+ Calculating Force | ||
| + | | style="height:20px; width:200px; text-align:center;" |A bow with a spring constant of 400N/m is stretched 0.5m. Calculate the force applied in the bow. | ||
| + | | style="height:20px; width:200px; text-align:center;" |A bungee cord with a spring constant of 45N/m stretches by 30m. Calculate the [[force]] applied to the cord. | ||
| + | | style="height:20px; width:200px; text-align:center;" |A slinky spring of length 10cm and spring constant 0.8N/m is stretched to a length of 10.1m. Calculate the [[force]] needed to stretch the slinky. | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities''' | ||
| + | |||
| + | Extension = 0.5m | ||
| + | |||
| + | Spring Constant = 400N/m | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities''' | ||
| + | |||
| + | Extension = 30m | ||
| + | |||
| + | Spring Constant = 45N/m | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities''' | ||
| + | |||
| + | Original Length = 10cm = 0.1m | ||
| + | |||
| + | New Length = 10.1m | ||
| + | |||
| + | Extension = 10.1 - 0.1 = 10m | ||
| + | |||
| + | Spring Constant = 0.8N/m | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math> F = kx </math> | ||
| + | |||
| + | <math> F = 400 \times 0.5 </math> | ||
| + | |||
| + | <math> F = 200N </math> | ||
| + | |||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math> F = kx </math> | ||
| + | |||
| + | <math> F = 45 \times 30 </math> | ||
| + | |||
| + | <math> F = 1350N </math> | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math> F = kx </math> | ||
| + | |||
| + | <math> F = 0.8 \times 10 </math> | ||
| + | |||
| + | <math> F = 8N </math> | ||
| + | |} | ||
| + | |||
| + | ==Key Stage 4== | ||
| + | ===Meaning=== | ||
| + | '''Hooke's Law''' states that the [[extension]] of an [[elastic]] [[object]] is [[Directly Proportional|directly proportional]] to the [[force]] applied to the [[object]]. | ||
| + | |||
| + | ===About Hooke's Law=== | ||
| + | : '''Hooke's Law''' describes how [[elastic]] [[object]]s behave when a pair of [[Equilibrium Forces|equilibrium forces]] is applied. | ||
| + | : '''Hooke's Law''' is described by the equation: Force = (Spring Constant) x (Extension) | ||
| + | : '''Hooke's Law''' applies to an [[object]] until it reaches its [[Elastic Limit|elastic limit]], at which point the [[object]] begins to behave [[Inelastic Deformation|plastically]]. | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |[[File:HookesLawSpring.png|center|400px]] | ||
| + | |- | ||
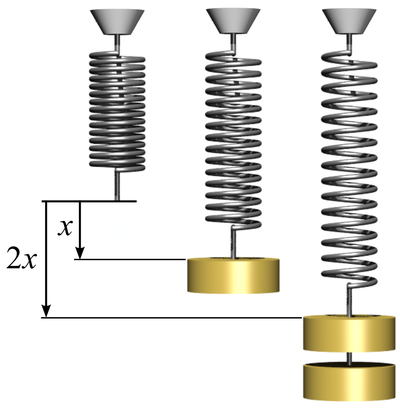
| + | | style="height:20px; width:200px; text-align:left;" |When a [[weight]] is added the spring [[Extension|extends]]. If the [[weight]] is doubled the [[extension]] is also doubled. | ||
| + | |} | ||
| + | : [[Elastic]] [[object]]s have an [[Elastic Limit]]. This means if the [[force]] is too big they stop obeying '''Hooke's Law''' and start to [[Deformation|deform]] [[Plastic (Property)|plastically]] so they will not return to their original shape. | ||
| + | |||
| + | ===Equation=== | ||
| + | Equilibrium Force = (Spring Constant) x (Extension of the Object) | ||
| + | |||
<math> F = kx </math> | <math> F = kx </math> | ||
<math> F = k \times x </math> | <math> F = k \times x </math> | ||
| − | Where | + | Where |
| − | + | ||
| − | + | <math>F</math> = [[Equilibrium Force]] applied | |
| − | + | ||
| + | <math>k</math> = [[Spring Constant]] (stiffness of the elastic object) | ||
| + | |||
| + | <math>x</math> = [[Extension]] of the [[object]] | ||
| + | |||
| + | ===Example Calculations=== | ||
| + | ====Calculating Equilibrium Force==== | ||
| + | {| class="wikitable" | ||
| + | | style="height:20px; width:200px; text-align:center;" |A bow with a spring constant of 390N/m is stretched 0.52m. Calculate the force applied in the bow correct to two [[Significant Figures|significant figures]]. | ||
| + | | style="height:20px; width:200px; text-align:center;" |A bungee cord with a spring constant of 45N/m stretches by 29m. Calculate the [[force]] applied to the cord correct to two [[Significant Figures|significant figures]]. | ||
| + | | style="height:20px; width:200px; text-align:center;" |A slinky spring of length 15cm and spring constant 0.87N/m is stretched to a length of 10m. Calculate the [[force]] needed to stretch the slinky correct to two [[Significant Figures|significant figures]]. | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities''' | ||
| + | |||
| + | Extension = 0.52m | ||
| + | |||
| + | Spring Constant = 390N/m | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities''' | ||
| + | |||
| + | Extension = 29m | ||
| + | |||
| + | Spring Constant = 45N/m | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities''' | ||
| + | |||
| + | Original Length = 15cm = 0.15m | ||
| + | |||
| + | New Length = 10m | ||
| + | |||
| + | Extension = 10 - 0.15 = 9.85m | ||
| + | |||
| + | Spring Constant = 0.87N/m | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math> F = kx </math> | ||
| + | |||
| + | <math> F = 390 \times 0.52 </math> | ||
| + | |||
| + | <math> F = 202.8N </math> | ||
| + | |||
| + | <math> F \approx 200N </math> | ||
| + | |||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math> F = kx </math> | ||
| + | |||
| + | <math> F = 45 \times 29 </math> | ||
| + | |||
| + | <math> F = 1305N </math> | ||
| + | |||
| + | <math> F \approx 1300N </math> | ||
| + | |||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math> F = kx </math> | ||
| + | |||
| + | <math> F = 0.87 \times 9.85 </math> | ||
| + | |||
| + | <math> F = 8.5695N </math> | ||
| + | |||
| + | <math> F \approx 8.6N </math> | ||
| + | |} | ||
| + | |||
| + | ====Calculating Spring Constant==== | ||
| + | {| class="wikitable" | ||
| + | | style="height:20px; width:200px; text-align:center;" |A car weighing 19000N rests on a single suspension spring. This causes the spring to shorten by 0.15m. Calculate the spring constant of this spring correct to two [[Significant Figure|significant figures]]. | ||
| + | | style="height:20px; width:200px; text-align:center;" |A girl of weight 360N balances perfectly on a pogo stick. When she is on the stick it is 13cm shorter than when she steps off. Calculate the spring constant of this spring correct to two [[Significant Figure|significant figures]]. | ||
| + | | style="height:20px; width:200px; text-align:center;" |A horse trailer of height 3.66m has 4 wheels, each with a suspension spring. When a horse which weighs 6200N gets on the trailer the height is reduced to 3.61m. Calculate the spring constant of each spring correct to two [[Significant Figure|significant figures]]. | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities''' | ||
| + | |||
| + | Extension = 0.15m | ||
| + | |||
| + | Force = 19000 | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities''' | ||
| + | |||
| + | Extension = 13cm = 0.13m | ||
| + | |||
| + | Force = 360N | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities''' | ||
| + | Original Length = 3.66m | ||
| + | |||
| + | Final Length = 3.61m | ||
| + | |||
| + | Extension = 0.05m | ||
| + | |||
| + | Force = 6200N | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers and [[Evaluate (Maths)|evaluate]].''' | ||
| + | |||
| + | <math> F = kx </math> | ||
| + | |||
| + | <math> 19000 = k \times 0.15 </math> | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers and [[Evaluate (Maths)|evaluate]].''' | ||
| + | |||
| + | <math> F = kx </math> | ||
| + | |||
| + | <math> 360 = k \times 0.13 </math> | ||
| + | |||
| + | | style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers and [[Evaluate (Maths)|evaluate]].''' | ||
| + | |||
| + | <math> F = kx </math> | ||
| + | |||
| + | <math> 6200 = k \times 0.05 </math> | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''3. [[Rearrange (Maths)|Rearrange]] the equation and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math> k = \frac{19000}{0.15} </math> | ||
| + | |||
| + | <math> k = 126666.7N/m </math> | ||
| + | |||
| + | <math> k \approx 130000N/m </math> | ||
| + | |||
| + | | style="height:20px; width:200px; text-align:left;" |'''3. [[Rearrange (Maths)|Rearrange]] the equation and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math> k = \frac{360}{0.13} </math> | ||
| + | |||
| + | <math> k = 2769.23N/m </math> | ||
| + | |||
| + | <math> k \approx 2800N/m </math> | ||
| + | | style="height:20px; width:200px; text-align:left;" |'''3. [[Rearrange (Maths)|Rearrange]] the equation and [[Solve (Maths)|solve]].''' | ||
| + | |||
| + | <math> k = \frac{6200}{0.05} </math> | ||
| + | |||
| + | <math> k = 124000N/m </math> | ||
| + | |||
| + | <math> k \approx 120000N/m </math> | ||
| + | |} | ||
| + | |||
| + | ===References=== | ||
| + | ====AQA==== | ||
| + | |||
| + | :[https://www.amazon.co.uk/gp/product/019835939X/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=019835939X&linkCode=as2&tag=nrjc-21&linkId=57e96876985fc39b1a3d8a3e3dc238b6 ''Hooke’s Law, pages 13, 159, GCSE Physics; Third Edition, Oxford University Press, AQA ''] | ||
| + | :[https://www.amazon.co.uk/gp/product/0008158770/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=0008158770&linkCode=as2&tag=nrjc-21&linkId=ec31595e720e1529e49876c3866fff6e ''Hooke's Law, pages 178-9, GCSE Physics; Student Book, Collins, AQA ''] | ||
| + | |||
| + | ====OCR==== | ||
| + | :[https://www.amazon.co.uk/gp/product/0198359837/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=0198359837&linkCode=as2&tag=nrjc-21&linkId=3c4229e8b023b2b60768e7ea2307cc6f ''Hooke`s law, pages 79, 253, 289, Gateway GCSE Physics, Oxford, OCR ''] | ||
| + | :[https://www.amazon.co.uk/gp/product/1782945695/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945695&linkCode=as2&tag=nrjc-21&linkId=ceafcc80bcad6b6754ee97a0c7ceea53 ''Hooke’s Law, pages 170-173, Gateway GCSE Combined Science; The Revision Guide, CGP, OCR ''] | ||
| + | :[https://www.amazon.co.uk/gp/product/1782945687/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945687&linkCode=as2&tag=nrjc-21&linkId=9a598e52189317a20311d7a632747bc9 ''Hooke’s Law, pages 36, 37, Gateway GCSE Physics; The Revision Guide, CGP, OCR ''] | ||
Latest revision as of 14:18, 22 December 2019
Contents
Key Stage 3
Meaning
Hooke's Law states that the extension of an elastic object is proportional to the force applied to the object.
About Hooke's Law
- Hooke's Law describes how elastic objects behave when a pair of opposing forces, one at each end of the object, are applied.
- Hooke's Law is described by the equation: Force = (Spring Constant) x (Extension)
| When a weight is added the spring extends. If the weight is doubled the extension is also doubled. |
- Elastic objects have an Elastic Limit. This means if the force is too big they stop obeying Hooke's Law and start to deform plastically so they will not return to their original shape.
Equation
Force = (Spring Constant) x (Extension of the spring)
\( F = kx \)
\( F = k \times x \)
Where
\(F\) = Force applied
\(k\) = Spring Constant (stiffness of the elastic object)
\(x\) = Extension of the object
Example Calculations
| A bow with a spring constant of 400N/m is stretched 0.5m. Calculate the force applied in the bow. | A bungee cord with a spring constant of 45N/m stretches by 30m. Calculate the force applied to the cord. | A slinky spring of length 10cm and spring constant 0.8N/m is stretched to a length of 10.1m. Calculate the force needed to stretch the slinky. |
| 1. State the known quantities
Extension = 0.5m Spring Constant = 400N/m |
1. State the known quantities
Extension = 30m Spring Constant = 45N/m |
1. State the known quantities
Original Length = 10cm = 0.1m New Length = 10.1m Extension = 10.1 - 0.1 = 10m Spring Constant = 0.8N/m |
| 2. Substitute the numbers into the equation and solve.
\( F = kx \) \( F = 400 \times 0.5 \) \( F = 200N \) |
2. Substitute the numbers into the equation and solve.
\( F = kx \) \( F = 45 \times 30 \) \( F = 1350N \) |
2. Substitute the numbers into the equation and solve.
\( F = kx \) \( F = 0.8 \times 10 \) \( F = 8N \) |
Key Stage 4
Meaning
Hooke's Law states that the extension of an elastic object is directly proportional to the force applied to the object.
About Hooke's Law
- Hooke's Law describes how elastic objects behave when a pair of equilibrium forces is applied.
- Hooke's Law is described by the equation: Force = (Spring Constant) x (Extension)
- Hooke's Law applies to an object until it reaches its elastic limit, at which point the object begins to behave plastically.
| When a weight is added the spring extends. If the weight is doubled the extension is also doubled. |
- Elastic objects have an Elastic Limit. This means if the force is too big they stop obeying Hooke's Law and start to deform plastically so they will not return to their original shape.
Equation
Equilibrium Force = (Spring Constant) x (Extension of the Object)
\( F = kx \)
\( F = k \times x \)
Where
\(F\) = Equilibrium Force applied
\(k\) = Spring Constant (stiffness of the elastic object)
\(x\) = Extension of the object
Example Calculations
Calculating Equilibrium Force
| A bow with a spring constant of 390N/m is stretched 0.52m. Calculate the force applied in the bow correct to two significant figures. | A bungee cord with a spring constant of 45N/m stretches by 29m. Calculate the force applied to the cord correct to two significant figures. | A slinky spring of length 15cm and spring constant 0.87N/m is stretched to a length of 10m. Calculate the force needed to stretch the slinky correct to two significant figures. |
| 1. State the known quantities
Extension = 0.52m Spring Constant = 390N/m |
1. State the known quantities
Extension = 29m Spring Constant = 45N/m |
1. State the known quantities
Original Length = 15cm = 0.15m New Length = 10m Extension = 10 - 0.15 = 9.85m Spring Constant = 0.87N/m |
| 2. Substitute the numbers into the equation and solve.
\( F = kx \) \( F = 390 \times 0.52 \) \( F = 202.8N \) \( F \approx 200N \) |
2. Substitute the numbers into the equation and solve.
\( F = kx \) \( F = 45 \times 29 \) \( F = 1305N \) \( F \approx 1300N \) |
2. Substitute the numbers into the equation and solve.
\( F = kx \) \( F = 0.87 \times 9.85 \) \( F = 8.5695N \) \( F \approx 8.6N \) |
Calculating Spring Constant
| A car weighing 19000N rests on a single suspension spring. This causes the spring to shorten by 0.15m. Calculate the spring constant of this spring correct to two significant figures. | A girl of weight 360N balances perfectly on a pogo stick. When she is on the stick it is 13cm shorter than when she steps off. Calculate the spring constant of this spring correct to two significant figures. | A horse trailer of height 3.66m has 4 wheels, each with a suspension spring. When a horse which weighs 6200N gets on the trailer the height is reduced to 3.61m. Calculate the spring constant of each spring correct to two significant figures. |
| 1. State the known quantities
Extension = 0.15m Force = 19000 |
1. State the known quantities
Extension = 13cm = 0.13m Force = 360N |
1. State the known quantities
Original Length = 3.66m Final Length = 3.61m Extension = 0.05m Force = 6200N |
| 2. Substitute the numbers and evaluate.
\( F = kx \) \( 19000 = k \times 0.15 \) |
2. Substitute the numbers and evaluate.
\( F = kx \) \( 360 = k \times 0.13 \) |
2. Substitute the numbers and evaluate.
\( F = kx \) \( 6200 = k \times 0.05 \) |
| 3. Rearrange the equation and solve.
\( k = \frac{19000}{0.15} \) \( k = 126666.7N/m \) \( k \approx 130000N/m \) |
3. Rearrange the equation and solve.
\( k = \frac{360}{0.13} \) \( k = 2769.23N/m \) \( k \approx 2800N/m \) |
3. Rearrange the equation and solve.
\( k = \frac{6200}{0.05} \) \( k = 124000N/m \) \( k \approx 120000N/m \) |
References
AQA
- Hooke’s Law, pages 13, 159, GCSE Physics; Third Edition, Oxford University Press, AQA
- Hooke's Law, pages 178-9, GCSE Physics; Student Book, Collins, AQA