Difference between revisions of "Resultant Force"
(→About Resultant Forces) |
|||
| Line 4: | Line 4: | ||
===About Resultant Forces=== | ===About Resultant Forces=== | ||
| − | : A '''resultant force''' can be calculated by taking [[force]]s that act in opposite | + | : A '''resultant force''' can be calculated by taking [[force]]s that act along the same line and add them together. |
| + | : If the [[force]]s are in the same direction as each other, then they have a [[Positive (Number)|value]]. | ||
| + | : If one [[force]] is acting in the opposite direction to another one of the [[force]]s is given a [[Negative (Number)|negative]] value. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |[[File:ForceNumberLineVertical.png|center|200px]] | ||
| + | | style="height:20px; width:300px; text-align:center;" |If the 'up' direction is chosen to be [[Positive (Number)|positive]] then any [[vector]] pointing 'up' has a [[Positive (Number)|positive]] value and any [[vector]] pointing 'down' has a [[Negative (Number)|negative]] value. | ||
| + | |||
| + | In this [[diagram]] the green [[vector]] has a value of +2 while the red [[vector]] has a value of -4. | ||
| + | |||
| + | If the number lines represent the number of [[Newton]]s [[force]] then the [[Resultant Force]] is the two values added together. | ||
| + | |||
| + | F<sub>Resultant</sub> = (+2N) + (-4N) | ||
| + | |||
| + | F<sub>Resultant</sub> = -2N upwards | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |[[File:ForceNumberLineHorizontal.png|center|400px]] | ||
| + | |- | ||
| + | | style="height:20px; width:400px; text-align:center;" |If the 'right' direction is chosen to be [[Positive (Number)|positive]] then any [[vector]] pointing 'right' has a [[Positive (Number)|positive]] value and any [[vector]] pointing 'left' has a [[Negative (Number)|negative]] value. | ||
| + | |||
| + | In this [[diagram]] the blue [[vector]] has a value of +3 while the yellow [[vector]] has a value of -2. | ||
| + | |||
| + | If the number lines represent the number of [[Newton]]s [[force]] then the [[Resultant Force]] is the two values added together. | ||
| + | |||
| + | F<sub>Resultant</sub> = (+3N) + (-2N) | ||
| + | |||
| + | F<sub>Resultant</sub> = 1N to the right | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |[[File:ForceNumberLineVertical.png|center|200px]] | ||
| + | | style="height:20px; width:300px; text-align:center;" |If the 'up' direction is chosen to be [[Positive (Number)|positive]] then any [[vector]] pointing 'up' has a [[Positive (Number)|positive]] value and any [[vector]] pointing 'down' has a [[Negative (Number)|negative]] value. | ||
| + | |||
| + | In this [[diagram]] the green [[vector]] has a value of +2 while the red [[vector]] has a value of -4. | ||
| + | |||
| + | If the number lines represent the number of [[Newton]]s [[force]] then the [[Resultant Force]] is the two values added together. | ||
| + | |||
| + | F<sub>Resultant</sub> = (+2N) + (-4N) | ||
| + | |||
| + | F<sub>Resultant</sub> = -2N upwards | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |[[File:ForceNumberLineHorizontal.png|center|400px]] | ||
| + | |- | ||
| + | | style="height:20px; width:400px; text-align:center;" |If the 'right' direction is chosen to be [[Positive (Number)|positive]] then any [[vector]] pointing 'right' has a [[Positive (Number)|positive]] value and any [[vector]] pointing 'left' has a [[Negative (Number)|negative]] value. | ||
| + | |||
| + | In this [[diagram]] the blue [[vector]] has a value of +3 while the yellow [[vector]] has a value of -2. | ||
| + | |||
| + | If the number lines represent the number of [[Newton]]s [[force]] then the [[Resultant Force]] is the two values added together. | ||
| + | |||
| + | F<sub>Resultant</sub> = (+3N) + (-2N) | ||
| + | |||
| + | F<sub>Resultant</sub> = 1N to the right | ||
| + | |} | ||
| + | |||
| + | ===Examples=== | ||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 12: | Line 76: | ||
|- | |- | ||
| style="height:20px; width:250px; text-align:left;" | | | style="height:20px; width:250px; text-align:left;" | | ||
| + | '''Choose which directions are [[Positive (Number)|positive]].''' | ||
| + | : Up is [[Positive (Number)|positive]]. | ||
| + | : Right is [[Positive (Number)|positive]]. | ||
| + | '''Calculate the [[Resultant Force]].''' | ||
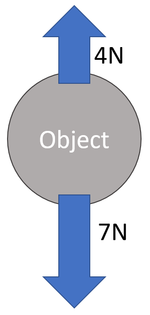
: There is 4[[N]] up and the 7[[N]] down. | : There is 4[[N]] up and the 7[[N]] down. | ||
| − | + | F<sub>Resultant</sub> = (+4N) + (-7N) | |
| − | + | ||
| + | F<sub>Resultant</sub> = -3N up | ||
| style="height:20px; width:250px; text-align:left;" | | | style="height:20px; width:250px; text-align:left;" | | ||
| + | '''Choose which directions are [[Positive (Number)|positive]].''' | ||
| + | : Up is [[Positive (Number)|positive]]. | ||
| + | : Right is [[Positive (Number)|positive]]. | ||
| + | '''Calculate the [[Resultant Force]].''' | ||
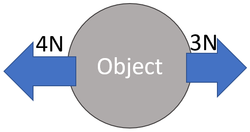
: There is 4[[N]] left and the 3[[N]] right. | : There is 4[[N]] left and the 3[[N]] right. | ||
| − | + | F<sub>Resultant</sub> = (+3N) + (-4N) | |
| − | + | ||
| + | F<sub>Resultant</sub> = -1N right | ||
| style="height:20px; width:250px; text-align:left;" | | | style="height:20px; width:250px; text-align:left;" | | ||
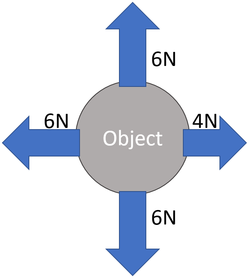
: There is 6[[N]] up and the 6[[N]] down. | : There is 6[[N]] up and the 6[[N]] down. | ||
Revision as of 15:19, 5 February 2019
Contents
Key Stage 3
Meaning
The Resultant Force is the overall force on an object.
About Resultant Forces
- A resultant force can be calculated by taking forces that act along the same line and add them together.
- If the forces are in the same direction as each other, then they have a value.
- If one force is acting in the opposite direction to another one of the forces is given a negative value.
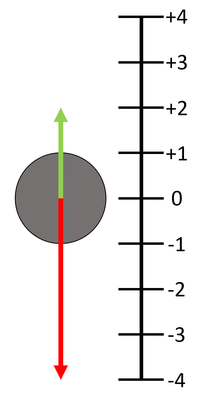
| If the 'up' direction is chosen to be positive then any vector pointing 'up' has a positive value and any vector pointing 'down' has a negative value.
In this diagram the green vector has a value of +2 while the red vector has a value of -4. If the number lines represent the number of Newtons force then the Resultant Force is the two values added together. FResultant = (+2N) + (-4N) FResultant = -2N upwards |
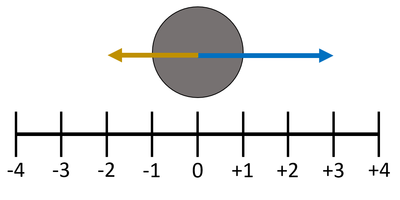
| If the 'right' direction is chosen to be positive then any vector pointing 'right' has a positive value and any vector pointing 'left' has a negative value.
In this diagram the blue vector has a value of +3 while the yellow vector has a value of -2. If the number lines represent the number of Newtons force then the Resultant Force is the two values added together. FResultant = (+3N) + (-2N) FResultant = 1N to the right |
| If the 'up' direction is chosen to be positive then any vector pointing 'up' has a positive value and any vector pointing 'down' has a negative value.
In this diagram the green vector has a value of +2 while the red vector has a value of -4. If the number lines represent the number of Newtons force then the Resultant Force is the two values added together. FResultant = (+2N) + (-4N) FResultant = -2N upwards |
| If the 'right' direction is chosen to be positive then any vector pointing 'right' has a positive value and any vector pointing 'left' has a negative value.
In this diagram the blue vector has a value of +3 while the yellow vector has a value of -2. If the number lines represent the number of Newtons force then the Resultant Force is the two values added together. FResultant = (+3N) + (-2N) FResultant = 1N to the right |
Examples
|
Choose which directions are positive. Calculate the Resultant Force. FResultant = (+4N) + (-7N) FResultant = -3N up |
Choose which directions are positive. Calculate the Resultant Force. FResultant = (+3N) + (-4N) FResultant = -1N right |
Key Stage 4
Meaning
The resultant force is the sum of all forces acting on an object.
About Resultant Forces
- When forces act in the same direction their magnitudes are added together.
- When forces act along the same line but in opposite directions; one is subtracted from the other.
- When forces are at right angles to one another they can be added using Pythagoras theorem to find the magnitude of the resultant force and then trigonometry can be used to find the direction of the resultant force.