Open main menu
Key Stage Wiki β

Difference between revisions of "Velocity-Time Graph"

(→‎Example Calculations)
 
(11 intermediate revisions by 2 users not shown)
Line 28: Line 28:
 
: The [[acceleration]] can be calculated from a '''velocity-time graph''' by reading the [[graph]] and using the equation <math>a=\frac{v-u}{t}</math>.
 
: The [[acceleration]] can be calculated from a '''velocity-time graph''' by reading the [[graph]] and using the equation <math>a=\frac{v-u}{t}</math>.
 
{| class="wikitable"
 
{| class="wikitable"
 +
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[acceleration]] of the object in this journey.'''
 +
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[acceleration]] of the object in this journey.'''
 
|-
 
|-
 
|[[File:vtGraphCalculateAcceleration1.png|center|300px]]
 
|[[File:vtGraphCalculateAcceleration1.png|center|300px]]
 
|[[File:vtGraphCalculateAcceleration2.png|center|300px]]
 
|[[File:vtGraphCalculateAcceleration2.png|center|300px]]
 
|-
 
|-
−
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[acceleration]] of the object in this journey.'''
+
| style="height:20px; width:300px; text-align:left;" |'''State the known [[variable]]s.'''
 +
v = 40m/s
 +
 
 +
u = 20m/s
 +
 
 +
t = 8s
 +
| style="height:20px; width:300px; text-align:left;" |'''State the known [[variable]]s.'''
 +
v = 10m/s
 +
 
 +
u = 40m/s
 +
 
 +
t = 8s
 +
|-
 +
| style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>a = \frac{v-u}{t}</math>
 +
 
 +
<math>a = \frac{40-20}{8}</math>
 +
 
 +
<math>a = \frac{20}{8}</math>
 +
 
 +
<math>a = 2.5m/s/s</math>
 +
| style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>a = \frac{v-u}{t}</math>
 +
 
 +
<math>a = \frac{10-40}{8}</math>
 +
 
 +
<math>a = \frac{-30}{8}</math>
 +
 
 +
<math>a = -3.75m/s/s</math>
 +
|}
 +
 
 +
{| class="wikitable"
 +
| style="height:20px; width:500px; text-align:left;" colspan = "3"|'''Calculate the [[acceleration]] of the [[object]] at each stage in this journey.'''
 +
|-
 +
| style="height:20px; width:500px; text-align:left;" colspan = "3"|[[File:vtGraph1.png|centre|500px]]
 +
|-
 +
| style="height:20px; width:300px; text-align:left;" |'''A'''
 +
| style="height:20px; width:300px; text-align:left;" |'''B'''
 +
| style="height:20px; width:300px; text-align:left;" |'''C'''
 +
|-
 +
| style="height:20px; width:300px; text-align:left;" |'''State the known [[variable]]s.'''
 +
[[File:vtGraphCalculateAcceleration3.png|centre|150px]]
 +
v = 30m/s
 +
 
 +
u = 0m/s
 +
 
 +
t = 2s
 +
| style="height:20px; width:300px; text-align:left;" |'''State the known [[variable]]s.'''
 +
[[File:vtGraphCalculateAcceleration3.png|centre|150px]]
 +
v = 30m/s
 +
 
 +
u = 30m/s
 +
 
 +
t = 3s
 +
| style="height:20px; width:300px; text-align:left;" |'''State the known [[variable]]s.'''
 +
[[File:vtGraphCalculateAcceleration3.png|centre|150px]]
 +
v = 50m/s
 +
 
 +
u = 30m/s
 +
 
 +
t = 3s
 +
|-
 +
| style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>a = \frac{v-u}{t}</math>
 +
 
 +
<math>a = \frac{30-0}{2}</math>
 +
 
 +
<math>a = \frac{30}{2}</math>
 +
 
 +
<math>a = 15m/s/s</math>
 +
| style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>a = \frac{v-u}{t}</math>
 +
 
 +
<math>a = \frac{30-30}{3}</math>
 +
 
 +
<math>a = \frac{0}{3}</math>
 +
 
 +
<math>a = 0m/s/s</math>
 +
| style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>a = \frac{v-u}{t}</math>
 +
 
 +
<math>a = \frac{50-30}{3}</math>
  
−
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[acceleration]] of the object in this journey.'''
+
<math>a = \frac{20}{3}</math>
  
 +
<math>a = 6.7m/s/s</math>
 
|}
 
|}
 +
 
====Calculating Distance Travelled====
 
====Calculating Distance Travelled====
−
: The [[distance]] travelled can be calculated from a '''velocity-time graph''' by breaking the [[graph]] into simple shapes and finding the [[area]] of those shapes. This may use the equations <math>a = b \times h</math> for rectangular shapes and <math>a = \frac{b \times h}{2}</math> for triangular shapes.
+
: The [[distance]] travelled can be calculated from a '''velocity-time graph''' by breaking the [[graph]] into simple shapes and finding the [[area]] of those shapes. This may use the equations <math>area = base \times height</math> for rectangular shapes and <math>area = \frac{base \times height}{2}</math> for triangular shapes.
  
 
{| class="wikitable"
 
{| class="wikitable"
 +
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[distance]] travelled by the [[object]] in this journey.'''
 +
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[distance]] travelled by the [[object]] in this journey.'''
 
|-
 
|-
 
|[[File:vtGraphCalculateArea1.png|center|300px]]
 
|[[File:vtGraphCalculateArea1.png|center|300px]]
 
|[[File:vtGraphCalculateArea2.png|center|300px]]
 
|[[File:vtGraphCalculateArea2.png|center|300px]]
 
|-
 
|-
−
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[distance]] travelled by the [[object]] in this journey.'''
+
| style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities'''
 +
base = 8s
 +
 
 +
height = 30m/s
 +
| style="height:20px; width:200px; text-align:left;" |'''1. State the known quantities'''
 +
base = 8s
 +
 
 +
height = 40m/s
 +
|-
 +
| style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>area = b \times h</math>
 +
 
 +
<math>area = 8 \times 30</math>
 +
 
 +
<math>area = distance = 250m</math>
 +
| style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>area = \frac{b \times h}{2}</math>
 +
 
 +
<math>area = \frac{8 \times 40}{2}</math>
 +
 
 +
<math>area = \frac{320}{2}</math>
 +
 
 +
<math>area = distance = 160m</math>
 +
|}
 +
 
 +
{| class="wikitable"
 +
| style="height:20px; width:500px; text-align:left;" colspan = "3"|'''Calculate the distance travelled by the [[object]] at each stage in this journey.'''
 +
|-
 +
| style="height:20px; width:500px; text-align:left;" colspan = "3"|[[File:vtGraph1.png|centre|500px]]
 +
|-
 +
| style="height:20px; width:300px; text-align:left;" |'''A'''
 +
| style="height:20px; width:300px; text-align:left;" |'''B'''
 +
| style="height:20px; width:300px; text-align:left;" |'''C'''
 +
|-
 +
| style="height:20px; width:300px; text-align:left;" |'''State the known [[variable]]s.'''
 +
[[File:vtGraphCalculateArea3.png|centre|150px]]
 +
b = 2s
 +
 
 +
h = 30m/s
 +
| style="height:20px; width:300px; text-align:left;" |'''State the known [[variable]]s.'''
 +
[[File:vtGraphCalculateArea3.png|centre|150px]]
 +
b = 3s
 +
 
 +
h = 30m/s
 +
| style="height:20px; width:300px; text-align:left;" |'''State the known [[variable]]s.'''
 +
[[File:vtGraphCalculateArea3.png|centre|150px]]
 +
b = 3s
 +
 
 +
h<sub>1</sub> = 30m/s
 +
 
 +
h<sub>2</sub> = 50m/s
 +
|-
 +
| style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>area = \frac{b \times h}{2}</math>
 +
 
 +
<math>area = \frac{2 \times 30}{2}</math>
 +
 
 +
<math>area = \frac{60}{2}</math>
 +
 
 +
<math>area = distance = 30m</math>
 +
| style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>area = b \times h</math>
 +
 
 +
<math>area = 3 \times 30</math>
 +
 
 +
<math>area = distance = 90m</math>
 +
| style="height:20px; width:200px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers into the [[equation]] and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>area = b \times h</math>
 +
 
 +
<math>area = 3 \times 30</math>
 +
 
 +
<math>area = distance = 90m</math> for yellow shaded area.
 +
 
 +
<math>area = \frac{b \times h}{2}</math>
 +
 
 +
<math>area = \frac{3 \times (50-30)}{2}</math>
 +
 
 +
<math>area = \frac{60}{2}</math>
  
−
| style="height:20px; width:300px; text-align:left;" |'''Calculate the [[distance]] travelled by the [[object]] in this journey.'''
+
<math>area = distance = 30m</math> for red area.
  
 +
''Total distance = 120m''
 
|}
 
|}
 +
 +
===References===
 +
====AQA====
 +
 +
:[https://www.amazon.co.uk/gp/product/0008158770/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=0008158770&linkCode=as2&tag=nrjc-21&linkId=ec31595e720e1529e49876c3866fff6e ''Velocity-time graph, pages 148-9, GCSE Physics; Student Book, Collins, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1782945598/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945598&linkCode=as2&tag=nrjc-21&linkId=ad276ad49df77ab4b40ab4fd0fe10400 ''Velocity-time graphs, page 211, GCSE Combined Science; The Revision Guide, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/019835939X/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=019835939X&linkCode=as2&tag=nrjc-21&linkId=57e96876985fc39b1a3d8a3e3dc238b6 ''Velocity-time graphs, pages 136, 138-141, GCSE Physics; Third Edition, Oxford University Press, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1471851370/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1471851370&linkCode=as2&tag=nrjc-21&linkId=01c69b0ae058f809cf636033e6ba793e ''Velocity-time graphs, pages 152-3, GCSE Physics, Hodder, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1782946403/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782946403&linkCode=as2&tag=nrjc-21&linkId=32a0abb60dff015b15b50e9b1d7b4644 ''Velocity-time graphs, pages 155-157, GCSE Combined Science Trilogy; Physics, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1782945970/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945970&linkCode=as2&tag=nrjc-21&linkId=a120d24dcc7cc7a58192069a3aafc1d2 ''Velocity-time graphs, pages 186-188, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1471851362/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1471851362&linkCode=as2&tag=nrjc-21&linkId=7d78d70a2044ee9982dae010c94af92a ''Velocity-time graphs, pages 230-1, 234, GCSE Combined Science Trilogy 2, Hodder, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/178294558X/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=178294558X&linkCode=as2&tag=nrjc-21&linkId=f0dfb66dafcb0c6e9449e7b1a4ae1ac484 ''Velocity-time graphs, pages 62, 63, GCSE Physics; The Revision Guide, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1782946403/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782946403&linkCode=as2&tag=nrjc-21&linkId=32a0abb60dff015b15b50e9b1d7b4644 ''Velocity-time graphs; area under, pages 156, 157, GCSE Combined Science Trilogy; Physics, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1782945970/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945970&linkCode=as2&tag=nrjc-21&linkId=a120d24dcc7cc7a58192069a3aafc1d2 ''Velocity-time graphs; area under, pages 187, 188, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1782945970/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945970&linkCode=as2&tag=nrjc-21&linkId=a120d24dcc7cc7a58192069a3aafc1d2 ''Velocity-time graphs; for falling objects, page 192, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA '']
 +
 +
====OCR====
 +
:[https://www.amazon.co.uk/gp/product/1782945695/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945695&linkCode=as2&tag=nrjc-21&linkId=ceafcc80bcad6b6754ee97a0c7ceea53 ''Velocity-time graphs, page 162, Gateway GCSE Combined Science; The Revision Guide, CGP, OCR '']
 +
:[https://www.amazon.co.uk/gp/product/1782945687/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945687&linkCode=as2&tag=nrjc-21&linkId=9a598e52189317a20311d7a632747bc9 ''Velocity-time graphs, page 25, Gateway GCSE Physics; The Revision Guide, CGP, OCR '']

Latest revision as of 10:59, 25 December 2019

Contents

Key Stage 4

Meaning

A velocity-time graph is a graph that shows how the velocity of an object changes with time.

About Velocity Time Graphs

Velocity-time graphs give information about the journey taken by an object.
On a velocity-time graph the velocity is plotted on the y-axis and the time is plotted on the x-axis.
A velocity-time graph can be used to calculate the acceleration of an object or the distance travelled by the object.
The gradient of a velocity-time graph is the same as the acceleration.
The area under the curve on a velocity-time graph is the distance travelled by an object.
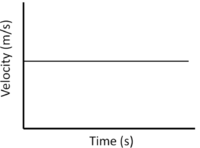
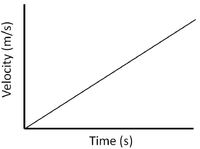
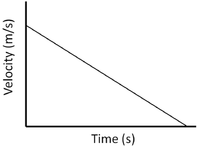
Constant Velocity Accelerating Decelerating
 
 
 
A gradient of zero shows the object is travelling at a constant velocity. Acceleration is shown by a positive gradient. Deceleration is shown by a negative gradient.

Example Calculations

Calculating Acceleration

The acceleration can be calculated from a velocity-time graph by reading the graph and using the equation \(a=\frac{v-u}{t}\).
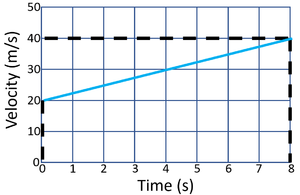
Calculate the acceleration of the object in this journey. Calculate the acceleration of the object in this journey.
 
 
State the known variables.

v = 40m/s

u = 20m/s

t = 8s

State the known variables.

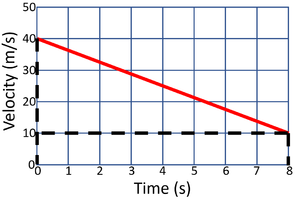
v = 10m/s

u = 40m/s

t = 8s

2. Substitute the numbers into the equation and solve.

\(a = \frac{v-u}{t}\)

\(a = \frac{40-20}{8}\)

\(a = \frac{20}{8}\)

\(a = 2.5m/s/s\)

2. Substitute the numbers into the equation and solve.

\(a = \frac{v-u}{t}\)

\(a = \frac{10-40}{8}\)

\(a = \frac{-30}{8}\)

\(a = -3.75m/s/s\)

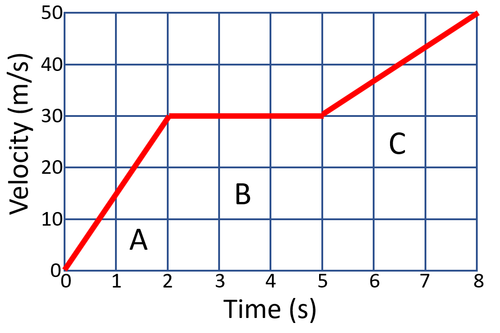
Calculate the acceleration of the object at each stage in this journey.
 
A B C
State the known variables.
 

v = 30m/s

u = 0m/s

t = 2s

State the known variables.
 

v = 30m/s

u = 30m/s

t = 3s

State the known variables.
 

v = 50m/s

u = 30m/s

t = 3s

2. Substitute the numbers into the equation and solve.

\(a = \frac{v-u}{t}\)

\(a = \frac{30-0}{2}\)

\(a = \frac{30}{2}\)

\(a = 15m/s/s\)

2. Substitute the numbers into the equation and solve.

\(a = \frac{v-u}{t}\)

\(a = \frac{30-30}{3}\)

\(a = \frac{0}{3}\)

\(a = 0m/s/s\)

2. Substitute the numbers into the equation and solve.

\(a = \frac{v-u}{t}\)

\(a = \frac{50-30}{3}\)

\(a = \frac{20}{3}\)

\(a = 6.7m/s/s\)

Calculating Distance Travelled

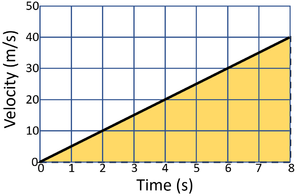
The distance travelled can be calculated from a velocity-time graph by breaking the graph into simple shapes and finding the area of those shapes. This may use the equations \(area = base \times height\) for rectangular shapes and \(area = \frac{base \times height}{2}\) for triangular shapes.
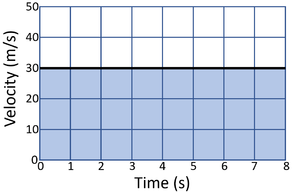
Calculate the distance travelled by the object in this journey. Calculate the distance travelled by the object in this journey.
 
 
1. State the known quantities

base = 8s

height = 30m/s

1. State the known quantities

base = 8s

height = 40m/s

2. Substitute the numbers into the equation and solve.

\(area = b \times h\)

\(area = 8 \times 30\)

\(area = distance = 250m\)

2. Substitute the numbers into the equation and solve.

\(area = \frac{b \times h}{2}\)

\(area = \frac{8 \times 40}{2}\)

\(area = \frac{320}{2}\)

\(area = distance = 160m\)

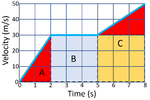
Calculate the distance travelled by the object at each stage in this journey.
 
A B C
State the known variables.
 

b = 2s

h = 30m/s

State the known variables.
 

b = 3s

h = 30m/s

State the known variables.
 

b = 3s

h1 = 30m/s

h2 = 50m/s

2. Substitute the numbers into the equation and solve.

\(area = \frac{b \times h}{2}\)

\(area = \frac{2 \times 30}{2}\)

\(area = \frac{60}{2}\)

\(area = distance = 30m\)

2. Substitute the numbers into the equation and solve.

\(area = b \times h\)

\(area = 3 \times 30\)

\(area = distance = 90m\)

2. Substitute the numbers into the equation and solve.

\(area = b \times h\)

\(area = 3 \times 30\)

\(area = distance = 90m\) for yellow shaded area.

\(area = \frac{b \times h}{2}\)

\(area = \frac{3 \times (50-30)}{2}\)

\(area = \frac{60}{2}\)

\(area = distance = 30m\) for red area.

Total distance = 120m

References

AQA

Velocity-time graph, pages 148-9, GCSE Physics; Student Book, Collins, AQA
Velocity-time graphs, page 211, GCSE Combined Science; The Revision Guide, CGP, AQA
Velocity-time graphs, pages 136, 138-141, GCSE Physics; Third Edition, Oxford University Press, AQA
Velocity-time graphs, pages 152-3, GCSE Physics, Hodder, AQA
Velocity-time graphs, pages 155-157, GCSE Combined Science Trilogy; Physics, CGP, AQA
Velocity-time graphs, pages 186-188, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
Velocity-time graphs, pages 230-1, 234, GCSE Combined Science Trilogy 2, Hodder, AQA
Velocity-time graphs, pages 62, 63, GCSE Physics; The Revision Guide, CGP, AQA
Velocity-time graphs; area under, pages 156, 157, GCSE Combined Science Trilogy; Physics, CGP, AQA
Velocity-time graphs; area under, pages 187, 188, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
Velocity-time graphs; for falling objects, page 192, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA

OCR

Velocity-time graphs, page 162, Gateway GCSE Combined Science; The Revision Guide, CGP, OCR
Velocity-time graphs, page 25, Gateway GCSE Physics; The Revision Guide, CGP, OCR
Retrieved from "https://keystagewiki.com/index.php?title=Velocity-Time_Graph&oldid=21690"