Balanced Forces
Contents
Key Stage 3
Meaning
Balanced Forces are forces that are the same strength but acting in opposite directions.
About Balanced Forces
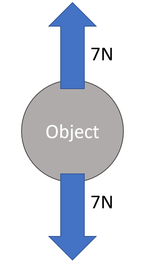
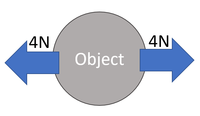
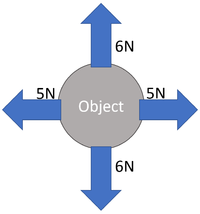
| The 7N up is balanced by the 7N down. | The 4N left is balanced by the 4N right. | The 6N up is balanced by the 6N down and the 5N left is balanced by the 5N right. |
Key Stage 4
Meaning
Balanced forces are force vectors which add together to make 0N resultant force.
About Balanced Forces
- When forces on an object are balanced there is no acceleration (change speed or direction).
- Balanced forces are related to Newton's First Law of motion:
- An object in motion will tend to stay in motion in a straight line and an object at rest will tend to stay at rest unless an unbalanced force acts upon it.
- If the resultant force on an object is zero, then the forces are balanced.
Examples
|
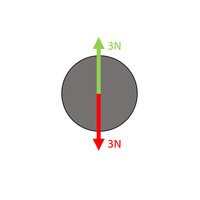
\(F_R = F_{up} - F_{down}\) \(F_R = 3 - 3\) \(F_R = 0N\) The forces are balanced. |
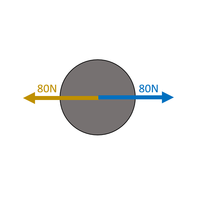
\(F_R = F_{right} - F_{left}\) \(F_R = 80 - 80\) \(F_R = 0N\) The forces are balanced. |
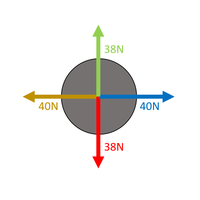
\(F_{Horiztonal} = F_{right} - F_{left}\) \(F_{Horiztonal} = 40 - 40\) \(F_{Horiztonal} = 0N\) \(F_{Vertical} = F_{up} - F_{down}\) \(F_{Vertical} = 38 - 38\) \(F_{Vertical} = 0N\) The forces are balanced. |
|
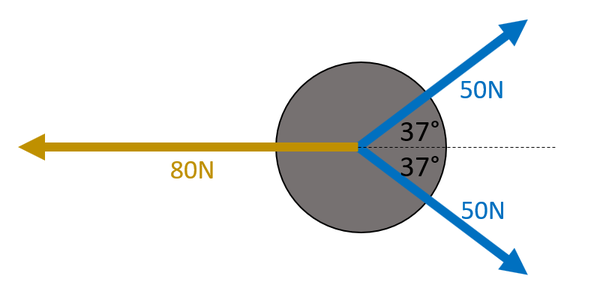
Whether these forces are balanced can be found by resolving the blue force vectors into the horizontal. See Resolving Forces. \(F_{right} = 50\cos37 + 50\cos37\) \(F_{right} = 79.86N\) Since the angle in the question is given to two significant figures the answer should also be quoted to two significant figures. \(F_{right} \approx 80N\) \(F_R = F_{right} - F_{left}\) \(F_R = 80 - 80\) \(F_R = 0N\) |
References
AQA
- Balanced forces, pages 114-133, GCSE Physics; Third Edition, Oxford University Press, AQA
- Balanced forces, pages 133, 170, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Balanced forces, pages 153, 166, 202, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Balanced forces, pages 154-6, GCSE Physics; Student Book, Collins, AQA