Motor Effect

Key Stage 4

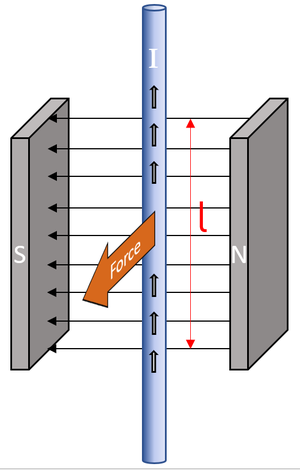
The motor effect is the force on a current carrying wire in a magnetic field.

When an a wire has an electrical current it has a magnetic field. If this wire is in the presence of an external magnetic field the two fields will interact causing a force.

The magnitude of the force depends upon:

The Current - The greater the current the greater the force.
The Magnetic Field - The greater the strength of magnetic field the greater the force.

The force on a current carrying wire is at right angles to both the current and the magnetic field.

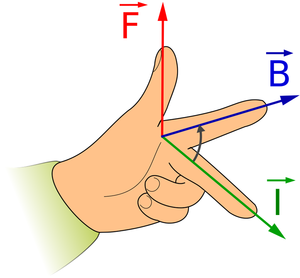
Fleming's Left Hand Rule can be used to find the direction of the force.


\(\overrightarrow{B}\): First finger field. \(\overrightarrow{I}\): Second finger current. \(\overrightarrow{F}\): The force.	The direction on the force on this wire can be found using Fleming's Left Hand Rule.

Force = (Magnetic Flux Density) x (Current) x (Length)

\(F = BIl\)

\(I\) = The Electrical Current through the wire.

\(l\) = The length of wire inside the magnetic field.

\(F\) = The force on the wire.

A wire carrying a current of 2.3A is inside a 55mT magnetic field that extends along the wire by a length of 6.1cm. Calculate the force on the wire correct to two significant figures.	23cm of wire carrying 1.2A of current is contained in a 37mT magnetic field. Calculate the force on the wire correct to two significant figures.
1. State the known quantities in SI Units. \(B\) = 55mT = 55x10^-3T \(I\) = 2.3A \(l\) = 6.1cm = 6.1x10^{-2^m}	1. State the known quantities in SI Units. \(B\) = 37mT = 37x10^-3T \(I\) = 1.2A \(l\) = 23cm = 23x10^{-2^m}
2. Substitute the numbers into the equation and solve. \(F = BIl\) \(F = 55\times 10^{-3} \times 2.3 \times 6.1 \times 10^{-2}\) \(F = 7.7165 \times 10^{-3}N\) \(F \approx 7.7\times 10^{-3}N\)	2. Substitute the numbers into the equation and solve. \(F = BIl\) \(F = 37\times 10^{-3} \times 1.2 \times 23 \times 10^{-2}\) \(F = 1.0212 \times 10^{-2}N\) \(F \approx 1.0\times 10^{-2}N\)