Electrical Resistance
Contents
Key Stage 3
Meaning
Resistance is a description of how difficult it is to increase the current through a conductor when increasing the potential difference.
About Resistance
- The unit of resistance is the Ohm (Ω).
- Resistance cannot be directly measured. Resistance must be calculated by dividing the Potential Difference by the Current.
- Conductors have a low resistance and insulators have a high resistance.
Equation
Resistance = (Potential Difference)/(Current)
\(R = \frac{V}{I}\)
Where
\(R\) = Resistance of a component.
\(V\) = The Potential Difference across the component.
\(I\) = The current through the component.
Example Calculations
| A student measures a potential difference of 5V across a component and a current of 0.1A. Calculate the resistance. | A bulb has a current of 200mA passing through it and a potential difference of 12V across it. Calculate the resistance of the bulb. | Calculate the resistance of a buzzer connected in series to a 6V battery with an ammeter reading of 10mA. |
|
Potential Difference = 5V Current = 0.1A \(R = \frac{V}{I}\) \(R = \frac{5}{0.1}\) \( R = 50 \Omega\) |
Potential Difference = 12V Current = 200mA = 0.2A \(R = \frac{V}{I}\) \(R = \frac{12}{0.2}\) \( R = 60 \Omega\) |
Potential Difference = 6V Current = 10mA = 0.01A \(R = \frac{V}{I}\) \(R = \frac{6}{0.01}\) \( R = 600 \Omega\) |
Key Stage 4
Meaning
Resistance is the ratio of potential difference to current.
About Resistance
- The unit of resistance is the Ohm (Ω).
- Resistance cannot be directly measured. Resistance must be calculated by dividing the Potential Difference by the Current.
- Conductors have a low resistance and insulators have a high resistance.
- Resistance in a wire is caused by electrons colliding with positive ions in the metal lattice.
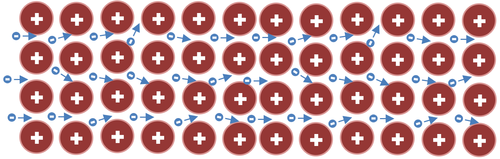
| This diagram shows electrons moving past the positive ions in a metal lattice. As they move some of them collide with the positive ions in the lattice which is acts as a resistance to an electrical current. |
- The higher the temperature of a conductor the greater the resistance of that conductor. This is due to the metal ions vibrating faster at higher temperatures which makes electrons more likely to collide with the ions as they pass through the conductor.
Equation
Resistance = (Potential Difference)/(Current)
\(R = \frac{V}{I}\)
Where
\(R\) = Resistance of a component.
\(V\) = The Potential Difference across the component.
\(I\) = The current through the component.
Example Calculations
Finding Resistance from Current and Potential Difference
| A student measures a potential difference of 5.9V across a component and a current of 0.11A. Calculate the resistance correct to two significant figures. | Calculate the resistance of a buzzer connected in series to a 9V battery with an ammeter reading of 23mA correct to two significant figures. |
| 1. State the known quantities in correct units.
Potential Difference = 5.9V Current = 0.11A |
1. State the known quantities in correct units.
Potential Difference = 9V Current = 23mA = 23x10-3A |
| 2. Substitute the numbers into the equation and solve.
\(R = \frac{V}{I}\) \(R = \frac{5.9}{0.11}\) \( R = 53.635 \Omega\) \( R \approx 54\Omega\) |
2. Substitute the numbers into the equation and solve.
\(R = \frac{V}{I}\) \(R = \frac{9}{23\times10^{-3}}\) \( R = 391.304 \Omega\) \( R \approx 390 \Omega\) |
Finding Current from Potential Difference and Resistance
| A potential difference of 9.9V is placed across an 19 Ohm resistor. Calculate the current flowing through the resistor correct to two significant figures. | A toaster has a resistance of 27 Ohms is plugged into the mains which has a potential difference of 230V. Calculate the current flowing through the toaster correct to two significant figures. |
| 1. State the known quantities in correct units.
V = 9.9V R = 19Ω |
1. State the known quantities in correct units.
V = 230V R = 27Ω |
| 2. Substitute the numbers and evaluate.
\(R = \frac{V}{I}\) \(19=\frac{9.9}{I}\) |
2. Substitute the numbers and evaluate.
\(R = \frac{V}{I}\) \(27=\frac{230}{R}\) |
| 3. Rearrange the equation and solve.
\(I=\frac{9.9}{19}\) \(I=0.52105A\) \(I\approx0.52A\) |
3. Rearrange the equation and solve.
\(I=\frac{230}{27}\) \(I=8.519A\) \(I\approx8.5A\) |
Finding Potential Difference from Current and Resistance
| A current of 55mA flows through a component with a resistance of 93 Ohms. Calculate the potential difference across this component correct to two significant figures. | A 22kΩ resistor has a current flowing through it of 6mA. Calculate the potential difference across the resistor correct to two significant figures. |
| 1. State the known quantities in correct units.
I = 55mA = 55x10-3A R = 93Ω |
1. State the known quantities in correct units.
I = 6mA = 6x10-3A R = 22kΩ = 22x103Ω |
| 2. Substitute the numbers and evaluate.
\(R = \frac{V}{I}\) \(93=\frac{V}{55 \times 10^{-3}}\) |
2. Substitute the numbers and evaluate.
\(R = \frac{V}{I}\) \(22 \times 10^3=\frac{V}{6 \times 10^{-3}}\) |
| 3. Rearrange the equation and solve.
\(V= 55 \times 10^{-3} \times 93\) \(V= 5.115V\) \(V\approx5.1V\) |
3. Rearrange the equation and solve.
\(V= 6 \times 10^{-3} \times 22 \times 10^3\) \(V= 132V\) \(V\approx130V\) |
References
AQA
- Resistance (electrical), page 63, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Resistance (electrical), page 65, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Resistance (electrical), pages 180-184, GCSE Combined Science; The Revision Guide, CGP, AQA
- Resistance (electrical), pages 24-30, 32, GCSE Physics; The Revision Guide, CGP, AQA
- Resistance (electrical); in parallel circuits, pages 186, 187, GCSE Combined Science; The Revision Guide, CGP, AQA
- Resistance (electrical); in parallel circuits, pages 29, 30, GCSE Physics; The Revision Guide, CGP, AQA
- Resistance (electrical); in parallel, pages 74, 77-79, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Resistance (electrical); in parallel, pages 76, 79-81, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Resistance (electrical); in series circuits, pages 185, 187, GCSE Combined Science; The Revision Guide, CGP, AQA
- Resistance (electrical); in series circuits, pages 28, 30, GCSE Physics; The Revision Guide, CGP, AQA
- Resistance (electrical); in series, pages 70, 77, 78, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Resistance (electrical); in series, pages 72, 79, 80, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Resistance (electrical); investigating, pages 64, 77-79, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Resistance (electrical); investigating, pages 66, 79-81, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Resistance (electrical); of diodes, page 66, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Resistance (electrical); of diodes, page 68, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Resistance (electrical); of filament lamps, page 66, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Resistance (electrical); of filament lamps, page 68, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Resistance (electrical); of LDRs, page 80, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Resistance (electrical); of LDRs, page 82, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Resistance (electrical); of resistors, pages 65, 66, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Resistance (electrical); of resistors, pages 67, 68, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Resistance (electrical); of thermistors, pages 80, 81, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Resistance (electrical); of thermistors, pages 82, 83, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Resistance (electrical); wire length, page 182, GCSE Combined Science; The Revision Guide, CGP, AQA