Contents
Key Stage 3
Meaning
Work Done is the amount of energy transferred by the action of a force.
About Work Done
- Work Done is measured in Joules.
- Work Done can only be calculated for objects moving in the direction of the force. If the direction of the force and the motion of an object are perpendicular then no work is being done on the object by that force.
Equation
Work Done = (Force) x (Distance moved in the direction of the force)
\( W = F \times d\)
\( W = Fd\)
- Work done is written with a capital W. Force is written with a capital F. Distance is written with a lower case d.
Example Calculations
| A person lifts a 40N box by a height of 1.2m. Calculate the work done by the person against gravity. | The brakes on a car apply a force of 10,000N. The car travels a distance of 15m braking. Calculate the work done by the brakes. | A person carries a 20N box along a horizontal path of 20m. |
|
Force = 40N Distance moved in the direction of the force = 1.2m \( W = Fd\) \( W = 40 \times 1.2\) \( W = 48J\) |
Force = 10,000N Distance moved in the direction of the force = 15m \( W = Fd\) \( W = 10,000 \times 15\) \( W = 15,000J\) |
Force = 40N Distance moved in the direction of the force = 0m \( W = Fd\) \( W = 20 \times 0\) \( W = 0J\) No work has been done because the movement is not in the direction of the force. The weight acts downwards but the movement was horizontal. |
Work Done by Deformation
- When an object is deformed, such as a spring being stretched, work is done to transfer energy into its Elastic Potential Energy Store.
Work Done on a Spring
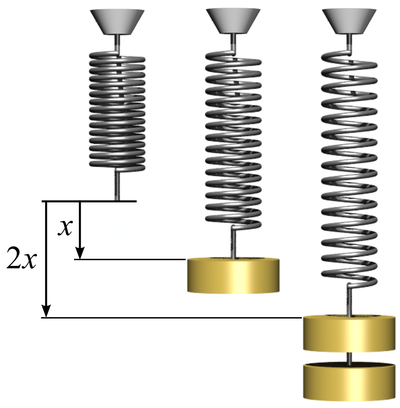
| Work is done to stretch this spring. |
The work done on a spring can be found with the following equation
\(W = \frac{1}{2} kx^2\)
Where:
W = Work Done
k = Spring Constant
Key Stage 4
Meaning
Work Done is the amount of energy transferred by the action of a force.
About Work Done
Work Done by a Force
- Work Done by a force can only be calculated for objects moving in the direction of the force. If the direction of the force and the motion of an object are perpendicular then no work is being done on the object by that force.
Work Done by Electricity
- Work can also be done by an electrical current as the electrostatic field inside a wire provides a force to move the electrons (or ions).
Equation for Work Done by a Force
Work Done = (Force) x (Distance moved in the direction of the force)
\( W = Fd\)
Where:
W = Work done
F = The Force applied to the object.
d = The distance moved by the object in the direction of the force.
Equation for Work Done by Electricity
Work Done = (Current) x (Potential Difference) x (time)
\( W = IVt\)
Where:
W = Work done
I = The current through the component
V = The potential difference across the component.
t = The length of time that the current is flowing.
NB: You do not need to remember this equation. However you do need to remember the two equations which are combined to make this equation.
1. \( P = IV\)
2. \( W = Pt\)
Where:
P = Power
Equation 1 is substituted into equation 2 to give \( W = IVt\).
Equation for Work Done by Deformation
\(W = \frac{1}{2} kx^2\)
Where:
W = Work Done
k = Spring Constant
References
AQA
- Work done, pages 18-21, 99, 170, GCSE Physics; Student Book, Collins, AQA
- Work done, pages 32, 33, 135, 136, GCSE Combined Science Trilogy; Physics, CGP, AQA
- Work done, pages 33, 34, 155, 156, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
- Work done, pages 8-9, GCSE Physics; Third Edition, Oxford University Press, AQA
Edexcel
- Work done, pages 130, 195, 201, GCSE Physics, Pearson Edexcel
- Work done; against friction, page 201, GCSE Physics, CGP, Edexcel
- Work done; by brakes, page 52, GCSE Physics, CGP, Edexcel
- Work done; by charges, pages 224, 242, GCSE Physics, CGP, Edexcel
- Work done; by forces, pages 62, 63, 199, GCSE Physics, CGP, Edexcel
- Work done; in stretching, page 325, GCSE Physics, CGP, Edexcel
- Work done; on gases, page 312, GCSE Physics, CGP, Edexcel