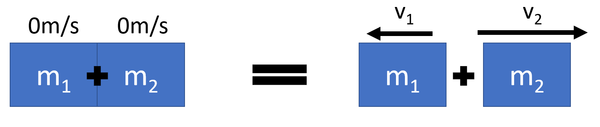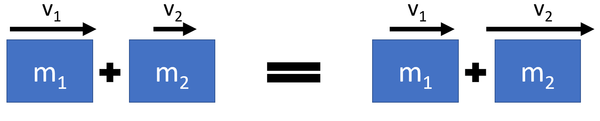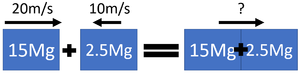Open main menu
Key Stage Wiki β

Difference between revisions of "Conservation of Momentum"
(→‎Inelastic Collisions)
 
(26 intermediate revisions by 2 users not shown)
Line 6: Line 6:
 
: '''Conservation of momentum''' means that if you add the [[momentum]] of every [[object]] before and event this will be the same as the total [[momentum]] after that event.
 
: '''Conservation of momentum''' means that if you add the [[momentum]] of every [[object]] before and event this will be the same as the total [[momentum]] after that event.
 
'''Conservation of momentum''' can be applied to 3 types of interaction to allow us to predict the outcome:
 
'''Conservation of momentum''' can be applied to 3 types of interaction to allow us to predict the outcome:
−
*Explosions - When two [[object]]s begin with zero [[momentum]] but are [[force]]d apart in opposite directions.
+
*[[Explosion (Momentum)|Explosion]]s - When two [[object]]s begin with zero [[momentum]] but are [[force]]d apart in opposite directions.
−
*Elastic Collisions - When two [[object]]s bounce off one another and the total [[Kinetic Energy Store|kinetic energy]] before a collision is the same as the total [[Kinetic Energy Store|kinetic energy]] after the collision.
+
*[[Elastic Collision]]s - When two [[object]]s bounce off one another and the total [[Kinetic Energy Store|kinetic energy]] before a [[Collide|collision]] is the same as the total [[Kinetic Energy Store|kinetic energy]] after the collision.
−
*Inelastic Collisions - When [[Kinetic Energy Store|kinetic energy]] is lost during a collision, often with the [[object]]s sticking together to form a larger [[object]].
+
*[[Inelastic Collision]]s - When [[Kinetic Energy Store|kinetic energy]] is lost during a [[Collide|collision]], often with the [[object]]s sticking together to form a larger [[object]].
  
 
===Equation===
 
===Equation===
Line 17: Line 17:
 
<math>p_{before} = p_{after}</math>
 
<math>p_{before} = p_{after}</math>
  
−
Where:
+
Where
  
 
<math>p_{before}</math> = The total [[momentum]] before an interaction.
 
<math>p_{before}</math> = The total [[momentum]] before an interaction.
Line 24: Line 24:
  
 
===Explosions===
 
===Explosions===
−
: During an explosion a single [[object]] with zero [[momentum]] splits into two smaller [[object]s.
+
: During an explosion a single [[object]] with zero [[momentum]] splits into two smaller [[object]]s.
 
: The total [[momentum]] before the explosion is zero. Due to '''conservation of momentum''' the total [[momentum]] after the explosion is also zero.
 
: The total [[momentum]] before the explosion is zero. Due to '''conservation of momentum''' the total [[momentum]] after the explosion is also zero.
  
 
<math>p_{before} = p_{after}</math>
 
<math>p_{before} = p_{after}</math>
  
−
Since:
+
Since
  
 
<math>p = mv</math>
 
<math>p = mv</math>
Line 35: Line 35:
 
Then:
 
Then:
  
 +
{| class="wikitable"
 +
|-
 +
|[[File:ConservationofMomentumExplosion.png|center|600px]]
 +
|}
 
<math>0 = m_1 v_1 + m_2 v_2</math>
 
<math>0 = m_1 v_1 + m_2 v_2</math>
  
−
Where:
+
Where
  
 
<math>m_1</math> = The [[mass]] of [[object]] 1.
 
<math>m_1</math> = The [[mass]] of [[object]] 1.
Line 46: Line 50:
  
 
<math>v_2</math> = The [[velocity]] of [[object]] 2 after the explosion.
 
<math>v_2</math> = The [[velocity]] of [[object]] 2 after the explosion.
 +
 +
{| class="wikitable"
 +
|-
 +
|[[File:Explosion.gif|center]]
 +
|}
  
 
====Example Explosion Calculations====
 
====Example Explosion Calculations====
Line 52: Line 61:
 
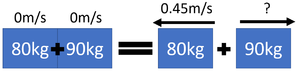
| style="height:20px; width:300px; text-align:center;" |An 80kg ice skater and a 90kg ice skater begin at rest and then push away from one another. The 80kg ice skater moves away with a velocity of 0.45m/s. Calculate the [[velocity]] of the 90kg ice skater correct to two [[Significant Figures|significant figures]].
 
| style="height:20px; width:300px; text-align:center;" |An 80kg ice skater and a 90kg ice skater begin at rest and then push away from one another. The 80kg ice skater moves away with a velocity of 0.45m/s. Calculate the [[velocity]] of the 90kg ice skater correct to two [[Significant Figures|significant figures]].
 
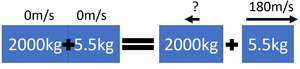
| style="height:20px; width:300px; text-align:center;" |An 18th century cannon of [[mass]] 2000kg fires a 5.5kg cannon ball at a [[velocity]] of 180m/s. Calculate the recoil [[velocity]] of the cannon correct to two [[Significant Figures|significant figures]].
 
| style="height:20px; width:300px; text-align:center;" |An 18th century cannon of [[mass]] 2000kg fires a 5.5kg cannon ball at a [[velocity]] of 180m/s. Calculate the recoil [[velocity]] of the cannon correct to two [[Significant Figures|significant figures]].
 +
|-
 +
|[[File:CofMCalc1.png|center|300px]]
 +
|[[File:CofMCalc2.png|center|300px]]
 
|-
 
|-
 
| style="height:20px; width:300px; text-align:left;" |'''1. State the known quantities'''
 
| style="height:20px; width:300px; text-align:left;" |'''1. State the known quantities'''
Line 116: Line 128:
 
<math>p_{before} = p_{after}</math>
 
<math>p_{before} = p_{after}</math>
  
−
Since:
+
Since
 +
 
 +
<math>p = mv</math>
 +
 
 +
Then:
 +
{| class="wikitable"
 +
|-
 +
|[[File:ConservationofMomentumElasticCollision.png|center|600px]]
 +
|}
 +
<math>m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4</math>
 +
 
 +
Where
 +
 
 +
<math>m_1</math> = The [[mass]] of [[object]] 1.
 +
 
 +
<math>v_1</math> = The [[velocity]] of [[object]] 1 before the collision.
 +
 
 +
<math>v_3</math> = The [[velocity]] of [[object]] 1 after the collision.
 +
 
 +
<math>m_2</math> = The [[mass]] of [[object]] 2.
 +
 
 +
<math>v_2</math> = The [[velocity]] of [[object]] 2 before the collision.
 +
 
 +
<math>v_4</math> = The [[velocity]] of [[object]] 2 after the collision.
 +
 
 +
{| class="wikitable"
 +
|-
 +
|[[File:ElasticCollision.gif|center]]
 +
|}
 +
 
 +
====Example Elastic Collision Calculations====
 +
{| class="wikitable"
 +
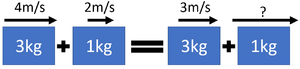
| style="height:20px; width: 300px; text-align:center;" |A trolley of [[mass]] 3kg travels at a [[velocity]] of 4m/s before colliding with a trolley of [[mass]] 1kg travelling in the same direction with a [[velocity]] of 2m/s. After the collision the 3kg trolley is moving with a [[velocity]] of 3m/s. Calculate the [[velocity]] of the 1kg trolley after the collision.
 +
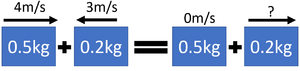
| style="height:20px; width: 300px; text-align:center;" |A rubber ball of [[mass]] 0.5kg travels at a [[speed]] of 4m/s towards another rubber ball, of [[mass]] 0.2kg traveling in the opposite direction with a [[speed]] of 3m/s. The 0.5kg rubber ball stops completely. Calculate the [[velocity]] of the 0.2kg rubber ball after the collision.
 +
|-
 +
|[[File:CofMCalc3.png|center|300px]]
 +
|[[File:CofMCalc4.png|center|300px]]
 +
|-
 +
| style="height:20px; width: 300px; text-align:left;" |'''1. State the known quantities'''
 +
 
 +
m<sub>1</sub> = 3kg
 +
 
 +
v<sub>1</sub> = 4m/s
 +
 
 +
v<sub>3</sub> = 3m/s
 +
 
 +
m<sub>2</sub> = 1kg
 +
 
 +
v<sub>2</sub> = 2m/s
 +
 
 +
| style="height:20px; width: 300px; text-align:left;" |'''1. State the known quantities'''
 +
 
 +
m<sub>1</sub> = 0.5kg
 +
 
 +
v<sub>1</sub> = 4m/s
 +
 
 +
v<sub>3</sub> = 0m/s
 +
 
 +
m<sub>2</sub> = 0.2kg
 +
 
 +
v<sub>2</sub> = -3m/s This is negative because it is travelling in the opposite direction.
 +
|-
 +
| style="height:20px; width: 300px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers and [[Evaluate (Maths)|evaluate]].'''
 +
 
 +
<math>m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4</math>
 +
 
 +
<math>3 \times 4 + 1 \times 2 = 3 \times 3 + 1 \times v_4</math>
 +
 
 +
<math>12 + 2 = 9 + v_4</math>
 +
 
 +
<math>14 = 9 + v_4</math>
 +
| style="height:20px; width: 300px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers and [[Evaluate (Maths)|evaluate]].'''
 +
 
 +
<math>m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4</math>
 +
 
 +
<math>0.5 \times 4 + 0.2 \times (-3) = 0.5 \times 0 + 0.2 \times v_4</math>
 +
 
 +
<math>2 -0.6 = 0 + 0.2v_4</math>
 +
 
 +
<math>1.4 = 0.2v_4</math>
 +
|-
 +
| style="height:20px; width: 300px; text-align:left;" |'''3. [[Rearrange (Maths)|Rearrange]] the equation and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>v_4 = 14-9</math>
 +
 
 +
<math>v_4 = 5m/s</math>
 +
| style="height:20px; width: 300px; text-align:left;" |'''3. [[Rearrange (Maths)|Rearrange]] the equation and [[Solve (Maths)|solve]].'''
 +
<math>v_4 = \frac{1.4}{0.2}</math>
 +
 
 +
<math>v_4 = 7m/s</math>
 +
|}
 +
 
 +
===Inelastic Collisions===
 +
: During inelastic collisions [[Kinetic Energy Store|kinetic energy]] is not conserved, so the total [[Kinetic Energy Store|kinetic energy]] before is greater than the total [[Kinetic Energy Store|kinetic energy]] after the collision.
 +
: During perfectly inelastic collisions the [[object]]s stick together.
 +
 
 +
<math>p_{before} = p_{after}</math>
 +
 
 +
Since
 +
 
 +
<math>p = mv</math>
 +
 
 +
Then
 +
{| class="wikitable"
 +
|-
 +
|[[File:ConservationofMomentumInelasticCollision.png|center|600px]]
 +
|}
 +
 
 +
<math>m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3</math>
 +
 
 +
Where
 +
 
 +
<math>m_1</math> = The [[mass]] of [[object]] 1.
 +
 
 +
<math>v_1</math> = The [[velocity]] of [[object]] 1 before the collision.
 +
 
 +
<math>m_2</math> = The [[mass]] of [[object]] 2.
 +
 
 +
<math>v_2</math> = The [[velocity]] of [[object]] 2 before the collision.
 +
 
 +
<math>v_3</math> = The [[velocity]] of new larger [[object]] after the collision.
 +
 
 +
{| class="wikitable"
 +
|-
 +
|[[File:InelasticCollision2.gif|center]]
 +
|}
 +
 
 +
{| class="wikitable"
 +
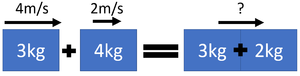
| style="height:20px; width: 300px; text-align:center;" |A trolley of [[mass]] 3kg travels at a [[velocity]] of 4m/s before colliding with a trolley of [[mass]] 1kg travelling in the same direction with a [[velocity]] of 2m/s. After the collision the two trolleys stick together. Calculate the [[velocity]] of the new larger trolley after the collision.
 +
| style="height:20px; width: 300px; text-align:center;" |A lorry of [[mass]] 15Mg travels at a [[speed]] of 20m/s towards a car, of [[mass]] 2500kg traveling in the opposite direction at 10m/s. In this collision the two vehicles stick together. Calculate the [[velocity]] of the combined vehicles after the collision correct to two [[Significant Figures|significant figures]].
 +
|-
 +
|[[File:CofMCalc5.png|center|300px]]
 +
|[[File:CofMCalc6.png|center|300px]]
 +
|-
 +
| style="height:20px; width: 300px; text-align:left;" |'''1. State the known quantities'''
 +
 
 +
m<sub>1</sub> = 3kg
 +
 
 +
v<sub>1</sub> = 4m/s
 +
 
 +
m<sub>2</sub> = 1kg
 +
 
 +
v<sub>2</sub> = 2m/s
 +
 
 +
| style="height:20px; width: 300px; text-align:left;" |'''1. State the known quantities'''
 +
 
 +
m<sub>1</sub> = 15Mg = 15x10<sup>3</sup>kg
 +
 
 +
v<sub>1</sub> = 4m/s
 +
 
 +
m<sub>2</sub> = 2.5x10<sup>3</sup>kg
 +
 
 +
v<sub>2</sub> = -10m/s This is negative because it is travelling in the opposite direction.
 +
|-
 +
| style="height:20px; width: 300px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers and [[Evaluate (Maths)|evaluate]].'''
 +
 
 +
<math>m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3</math>
 +
 
 +
<math>3 \times 4 + 1 \times 2 = (3+1) \times v_3</math>
 +
 
 +
<math>12 + 2 = 4v_3</math>
 +
 
 +
<math>14 = 4v_3</math>
 +
| style="height:20px; width: 300px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers and [[Evaluate (Maths)|evaluate]].'''
 +
 
 +
<math>m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3</math>
 +
 
 +
<math>15 \times 10^3 \times 20 + 2.5 \times 10^3 \times (-10) = ((15 \times 10^3) + (2.5 \times 10^3)) \times v_3</math>
 +
 
 +
<math>300000 - 25000 = 17500 \times v_3</math>
 +
 
 +
<math>275000 = 17500v_3</math>
 +
|-
 +
| style="height:20px; width: 300px; text-align:left;" |'''3. [[Rearrange (Maths)|Rearrange]] the equation and [[Solve (Maths)|solve]].'''
 +
 
 +
<math>v_3 = \frac{14}{4}</math>
 +
 
 +
<math>v_3 = 3.5m/s</math>
 +
| style="height:20px; width: 300px; text-align:left;" |'''3. [[Rearrange (Maths)|Rearrange]] the equation and [[Solve (Maths)|solve]].'''
 +
<math>v_3 = \frac{275000}{17500}</math>
 +
 
 +
<math>v_3 = 15.7142m/s</math>
 +
 
 +
<math>v_3 \approx 16m/s</math>
 +
|}
 +
 
 +
===References===
 +
====AQA====
 +
 
 +
:[https://www.amazon.co.uk/gp/product/1782946403/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782946403&linkCode=as2&tag=nrjc-21&linkId=32a0abb60dff015b15b50e9b1d7b4644 ''Conservation of momentum, page 183, GCSE Combined Science Trilogy; Physics, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1782945970/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945970&linkCode=as2&tag=nrjc-21&linkId=a120d24dcc7cc7a58192069a3aafc1d2 ''Conservation of momentum, page 216, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/019835939X/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=019835939X&linkCode=as2&tag=nrjc-21&linkId=57e96876985fc39b1a3d8a3e3dc238b6 ''Conservation of momentum, pages 150-153, 156-157, GCSE Physics; Third Edition, Oxford University Press, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/1471851370/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1471851370&linkCode=as2&tag=nrjc-21&linkId=01c69b0ae058f809cf636033e6ba793e ''Conservation of momentum, pages 169-70m GCSE Physics, Hodder, AQA '']
 +
:[https://www.amazon.co.uk/gp/product/178294558X/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=178294558X&linkCode=as2&tag=nrjc-21&linkId=f0dfb66dafcb0c6e9449e7b1a4ae1ac65 ''Conservation of momentum, pages 70, 71, GCSE Physics; The Revision Guide, CGP, AQA '']
 +
 
 +
====Edexcel====
 +
 
 +
:[https://www.amazon.co.uk/gp/product/1292120193/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1292120193&linkCode=as2&tag=nrjc-21&linkId=572df39392fb4200db8391d98ae6314e ''Conservation of momentum, law of, page 309, GCSE Combined Science, Pearson Edexcel '']
 +
:[https://www.amazon.co.uk/gp/product/1292120223/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1292120223&linkCode=as2&tag=nrjc-21&linkId=068ecf40278c32406a7f1c6e66751417 ''Conservation of momentum, page 25, GCSE Physics, Pearson Edexcel '']
 +
:[https://www.amazon.co.uk/gp/product/1782945741/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945741&linkCode=as2&tag=nrjc-21&linkId=30da4f2178da182547b62a7329d13b57 ''Conservation of momentum, pages 153, 154, GCSE Combined Science; The Revision Guide, CGP, Edexcel '']
 +
:[https://www.amazon.co.uk/gp/product/1782945733/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782945733&linkCode=as2&tag=nrjc-21&linkId=2a2dbec9db6bf5766c0458d908fa0a52 ''Conservation of momentum, pages 20, 21, GCSE Physics; The Revision Guide, CGP, Edexcel '']
 +
:[https://www.amazon.co.uk/gp/product/1782948163/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=1782948163&linkCode=as2&tag=nrjc-21&linkId=0fdbfd5dd397d6e24a9dfb250f08587f ''Conservation of momentum, pages 44, 45, GCSE Physics, CGP, Edexcel '']
 +
 
 +
====OCR====
 +
:[https://www.amazon.co.uk/gp/product/0198359837/ref=as_li_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=0198359837&linkCode=as2&tag=nrjc-21&linkId=3c4229e8b023b2b60768e7ea2307cc6f ''Law of conservation; Momentum, pages 72, Gateway GCSE Physics, Oxford, OCR '']
 +
 
 +
==Key Stage 5==
 +
===Meaning===
 +
The law of '''conservation of momentum''' is the observation that the total [[momentum]] in a [[Closed Isolated System|closed isolated system]] remains the same before and after any interaction between those [[particle]]s (provided no external [[Resultant Force|resultant forces]] acts upon that [[system]].
 +
 
 +
===About Conservation of Momentum===
 +
*'''Conservation of momentum''' applies to all types of [[Collide|collisions]] and interactions.
 +
*[[Momentum]] is a [[vector]] quantity, meaning it has both [[magnitude]] and direction.
 +
*'''Conservation of momentum''' indicates that the total [[momentum]] before an interaction is equal to the total [[momentum]] after the interaction.
 +
*'''Conservation of momentum''' is a fundamental principle in [[Mechanics (Physics)|mechanics]] and [[Dynamics (Physics)|dynamics]].
 +
*'''Conservation of momentum''' is used to analyse the motion of [[object]]s before and after [[Collide|collisions]].
 +
*'''Conservation of momentum''' is a consequence of [[Newton's Third Law|Newton's third law of motion]].
 +
*In a [[Fundamental Interactions|fundamental interaction]] between [[Subatomic Particle|subatomic particles]] '''momentum is conserved'''. This can be used to detect new [[Subatomic Particle|particles]] which cannot be seen in a cloud chamber. Any time a [[Fundamental Interactions|particle interaction]] appears to violate '''conservation of momentum''' it means that a new, unseen [[Subatomic Particle|particle]] has been created and carried away the [[momentum]].
 +
*'''Conservation of momentum''' is applied to calculations involving [[Elastic Collision|elastic collisions]], [[Inelastic Collision|inelastic collisions]] and [[Explosion (Momentum)|explosions]] to find unknown variables before of after the interaction.
 +
 
 +
===Formula===
 +
Total Momentum Before = Total Momentum After
 +
 
 +
<math>p_{before} = p_{after}</math>
 +
 
 +
Where
 +
 
 +
<math>p_{before}</math> = The total [[momentum]] before an interaction.
 +
 
 +
<math>p_{after}</math> = The total [[momentum]] after the interaction.
 +
 
 +
===Explosions===
 +
: During an explosion a single [[object]] with zero [[momentum]] splits into two smaller [[object]]s.
 +
: The total [[momentum]] before the explosion is zero. Due to '''conservation of momentum''' the total [[momentum]] after the explosion is also zero.
 +
 
 +
<math>p_{before} = p_{after}</math>
 +
 
 +
Since
  
 
<math>p = mv</math>
 
<math>p = mv</math>
Line 122: Line 371:
 
Then:
 
Then:
  
 +
{| class="wikitable"
 +
|-
 +
|[[File:ConservationofMomentumExplosion.png|center|600px]]
 +
|}
 +
<math>0 = m_1 v_1 + m_2 v_2</math>
 +
 +
Where
 +
 +
<math>m_1</math> = The [[mass]] of [[object]] 1.
 +
 +
<math>v_1</math> = The [[velocity]] of [[object]] 1 after the explosion.
 +
 +
<math>m_2</math> = The [[mass]] of [[object]] 2.
 +
 +
<math>v_2</math> = The [[velocity]] of [[object]] 2 after the explosion.
 +
 +
{| class="wikitable"
 +
|-
 +
|[[File:Explosion.gif|center]]
 +
|}
 +
 +
====Example Explosion Calculations====
 +
 +
{| class="wikitable"
 +
| style="height:20px; width:300px; text-align:center;" |An 80kg ice skater and a 90kg ice skater begin at rest and then push away from one another. The 80kg ice skater moves away with a velocity of 0.45m/s. Calculate the [[velocity]] of the 90kg ice skater correct to two [[Significant Figures|significant figures]].
 +
| style="height:20px; width:300px; text-align:center;" |An 18th century cannon of [[mass]] 2000kg fires a 5.5kg cannon ball at a [[velocity]] of 180m/s. Calculate the recoil [[velocity]] of the cannon correct to two [[Significant Figures|significant figures]].
 +
|-
 +
|[[File:CofMCalc1.png|center|300px]]
 +
|[[File:CofMCalc2.png|center|300px]]
 +
|-
 +
| style="height:20px; width:300px; text-align:left;" |'''1. State the known quantities'''
 +
 +
p<sub>before</sub> = 0kgm/s
 +
 +
m<sub>1</sub> = 80kg
 +
 +
m<sub>2</sub> = 90kg
 +
 +
v<sub>1</sub> = 0.45m/s
 +
| style="height:20px; width:300px; text-align:left;" |'''1. State the known quantities'''
 +
 +
p<sub>before</sub> = 0kgm/s
 +
 +
m<sub>1</sub> = 2000kg
 +
 +
m<sub>2</sub> = 5.5kg
 +
 +
v<sub>1</sub> = 180m/s
 +
|-
 +
| style="height:20px; width:300px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers and [[Evaluate (Maths)|evaluate]].'''
 +
 +
<math>p_{before} = p_{after}</math>
 +
 +
<math>0 = m_1 v_1 + m_2 v_2</math>
 +
 +
<math>0 = 80 \times 0.45 + 90 \times v_2</math>
 +
 +
<math>0 = 36 + 90v_2</math>
 +
 +
| style="height:20px; width:300px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers and [[Evaluate (Maths)|evaluate]].'''
 +
 +
<math>p_{before} = p_{after}</math>
 +
 +
<math>0 = m_1 v_1 + m_2 v_2</math>
 +
 +
<math>0 = 2000 \times v_1 + 5.5 \times 180</math>
 +
 +
<math>0 = 2000v_1 + 990</math>
 +
|-
 +
| style="height:20px; width:300px; text-align:left;" |'''3. [[Rearrange (Maths)|Rearrange]] the equation and [[Solve (Maths)|solve]].'''
 +
 +
<math>90v_2 = -36</math>
 +
 +
<math>v_2 = \frac{-36}{90}</math>
 +
 +
<math>v_2 = -0.40m/s</math>
 +
| style="height:20px; width:300px; text-align:left;" |'''3. [[Rearrange (Maths)|Rearrange]] the equation and [[Solve (Maths)|solve]].'''
 +
 +
<math>2000v_1 = -990</math>
 +
 +
<math>v_1 = \frac{-990}{2000}</math>
 +
 +
<math>v_1 = -0.495m/s</math>
 +
 +
<math>v_1 \approx -0.50m/s</math>
 +
|}
 +
 +
===Elastic Collisions===
 +
: During elastic collisions [[Kinetic Energy Store|kinetic energy]] is conserved, so the total [[Kinetic Energy Store|kinetic energy]] before the collision is equal to the total [[Kinetic Energy Store|kinetic energy]] after the collision.
 +
: During elastic collisions the [[object]]s bounce off one another.
 +
 +
<math>p_{before} = p_{after}</math>
 +
 +
Since
 +
 +
<math>p = mv</math>
 +
 +
Then:
 +
{| class="wikitable"
 +
|-
 +
|[[File:ConservationofMomentumElasticCollision.png|center|600px]]
 +
|}
 
<math>m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4</math>
 
<math>m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4</math>
  
−
Where:
+
Where
  
 
<math>m_1</math> = The [[mass]] of [[object]] 1.
 
<math>m_1</math> = The [[mass]] of [[object]] 1.
  
−
<math>v_1</math> = The [[velocity]] of [[object]] 1 before the explosion.
+
<math>v_1</math> = The [[velocity]] of [[object]] 1 before the collision.
  
−
<math>v_3</math> = The [[velocity]] of [[object]] 1 after the explosion.
+
<math>v_3</math> = The [[velocity]] of [[object]] 1 after the collision.
  
 
<math>m_2</math> = The [[mass]] of [[object]] 2.
 
<math>m_2</math> = The [[mass]] of [[object]] 2.
  
−
<math>v_2</math> = The [[velocity]] of [[object]] 2 before the explosion.
+
<math>v_2</math> = The [[velocity]] of [[object]] 2 before the collision.
  
−
<math>v_4</math> = The [[velocity]] of [[object]] 2 after the explosion.
+
<math>v_4</math> = The [[velocity]] of [[object]] 2 after the collision.
 +
 
 +
{| class="wikitable"
 +
|-
 +
|[[File:ElasticCollision.gif|center]]
 +
|}
  
 +
====Example Elastic Collision Calculations====
 
{| class="wikitable"
 
{| class="wikitable"
 
| style="height:20px; width: 300px; text-align:center;" |A trolley of [[mass]] 3kg travels at a [[velocity]] of 4m/s before colliding with a trolley of [[mass]] 1kg travelling in the same direction with a [[velocity]] of 2m/s. After the collision the 3kg trolley is moving with a [[velocity]] of 3m/s. Calculate the [[velocity]] of the 1kg trolley after the collision.
 
| style="height:20px; width: 300px; text-align:center;" |A trolley of [[mass]] 3kg travels at a [[velocity]] of 4m/s before colliding with a trolley of [[mass]] 1kg travelling in the same direction with a [[velocity]] of 2m/s. After the collision the 3kg trolley is moving with a [[velocity]] of 3m/s. Calculate the [[velocity]] of the 1kg trolley after the collision.
 
| style="height:20px; width: 300px; text-align:center;" |A rubber ball of [[mass]] 0.5kg travels at a [[speed]] of 4m/s towards another rubber ball, of [[mass]] 0.2kg traveling in the opposite direction with a [[speed]] of 3m/s. The 0.5kg rubber ball stops completely. Calculate the [[velocity]] of the 0.2kg rubber ball after the collision.
 
| style="height:20px; width: 300px; text-align:center;" |A rubber ball of [[mass]] 0.5kg travels at a [[speed]] of 4m/s towards another rubber ball, of [[mass]] 0.2kg traveling in the opposite direction with a [[speed]] of 3m/s. The 0.5kg rubber ball stops completely. Calculate the [[velocity]] of the 0.2kg rubber ball after the collision.
 +
|-
 +
|[[File:CofMCalc3.png|center|300px]]
 +
|[[File:CofMCalc4.png|center|300px]]
 
|-
 
|-
 
| style="height:20px; width: 300px; text-align:left;" |'''1. State the known quantities'''
 
| style="height:20px; width: 300px; text-align:left;" |'''1. State the known quantities'''
Line 197: Line 557:
  
 
===Inelastic Collisions===
 
===Inelastic Collisions===
 +
: During inelastic collisions [[Kinetic Energy Store|kinetic energy]] is not conserved, so the total [[Kinetic Energy Store|kinetic energy]] before is greater than the total [[Kinetic Energy Store|kinetic energy]] after the collision.
 +
: During perfectly inelastic collisions the [[object]]s stick together.
 +
 +
<math>p_{before} = p_{after}</math>
 +
 +
Since
 +
 +
<math>p = mv</math>
 +
 +
Then
 +
{| class="wikitable"
 +
|-
 +
|[[File:ConservationofMomentumInelasticCollision.png|center|600px]]
 +
|}
 +
 +
<math>m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3</math>
 +
 +
Where
 +
 +
<math>m_1</math> = The [[mass]] of [[object]] 1.
 +
 +
<math>v_1</math> = The [[velocity]] of [[object]] 1 before the collision.
 +
 +
<math>m_2</math> = The [[mass]] of [[object]] 2.
 +
 +
<math>v_2</math> = The [[velocity]] of [[object]] 2 before the collision.
 +
 +
<math>v_3</math> = The [[velocity]] of new larger [[object]] after the collision.
 +
 +
{| class="wikitable"
 +
|-
 +
|[[File:InelasticCollision2.gif|center]]
 +
|}
 +
 +
{| class="wikitable"
 +
| style="height:20px; width: 300px; text-align:center;" |A trolley of [[mass]] 3kg travels at a [[velocity]] of 4m/s before colliding with a trolley of [[mass]] 1kg travelling in the same direction with a [[velocity]] of 2m/s. After the collision the two trolleys stick together. Calculate the [[velocity]] of the new larger trolley after the collision.
 +
| style="height:20px; width: 300px; text-align:center;" |A lorry of [[mass]] 15Mg travels at a [[speed]] of 20m/s towards a car, of [[mass]] 2500kg traveling in the opposite direction at 10m/s. In this collision the two vehicles stick together. Calculate the [[velocity]] of the combined vehicles after the collision correct to two [[Significant Figures|significant figures]].
 +
|-
 +
|[[File:CofMCalc5.png|center|300px]]
 +
|[[File:CofMCalc6.png|center|300px]]
 +
|-
 +
| style="height:20px; width: 300px; text-align:left;" |'''1. State the known quantities'''
 +
 +
m<sub>1</sub> = 3kg
 +
 +
v<sub>1</sub> = 4m/s
 +
 +
m<sub>2</sub> = 1kg
 +
 +
v<sub>2</sub> = 2m/s
 +
 +
| style="height:20px; width: 300px; text-align:left;" |'''1. State the known quantities'''
 +
 +
m<sub>1</sub> = 15Mg = 15x10<sup>3</sup>kg
 +
 +
v<sub>1</sub> = 4m/s
 +
 +
m<sub>2</sub> = 2.5x10<sup>3</sup>kg
 +
 +
v<sub>2</sub> = -10m/s This is negative because it is travelling in the opposite direction.
 +
|-
 +
| style="height:20px; width: 300px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers and [[Evaluate (Maths)|evaluate]].'''
 +
 +
<math>m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3</math>
 +
 +
<math>3 \times 4 + 1 \times 2 = (3+1) \times v_3</math>
 +
 +
<math>12 + 2 = 4v_3</math>
 +
 +
<math>14 = 4v_3</math>
 +
| style="height:20px; width: 300px; text-align:left;" |'''2. [[Substitute (Maths)|Substitute]] the numbers and [[Evaluate (Maths)|evaluate]].'''
 +
 +
<math>m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3</math>
 +
 +
<math>15 \times 10^3 \times 20 + 2.5 \times 10^3 \times (-10) = ((15 \times 10^3) + (2.5 \times 10^3)) \times v_3</math>
 +
 +
<math>300000 - 25000 = 17500 \times v_3</math>
 +
 +
<math>275000 = 17500v_3</math>
 +
|-
 +
| style="height:20px; width: 300px; text-align:left;" |'''3. [[Rearrange (Maths)|Rearrange]] the equation and [[Solve (Maths)|solve]].'''
 +
 +
<math>v_3 = \frac{14}{4}</math>
 +
 +
<math>v_3 = 3.5m/s</math>
 +
| style="height:20px; width: 300px; text-align:left;" |'''3. [[Rearrange (Maths)|Rearrange]] the equation and [[Solve (Maths)|solve]].'''
 +
<math>v_3 = \frac{275000}{17500}</math>
 +
 +
<math>v_3 = 15.7142m/s</math>
 +
 +
<math>v_3 \approx 16m/s</math>
 +
|}

Latest revision as of 11:47, 23 May 2024

Key Stage 4 Higher

Meaning

The law of conservation of momentum is the fact that the total momentum in a closed isolated system remains the same before and after an interaction.

About Conservation of Momentum

Conservation of momentum means that if you add the momentum of every object before and event this will be the same as the total momentum after that event.

Conservation of momentum can be applied to 3 types of interaction to allow us to predict the outcome:

Equation

NB: You do not need to remember the equation but you must be able to apply the law of conservation of momentum.

Total Momentum Before = Total Momentum After

\(p_{before} = p_{after}\)

Where

\(p_{before}\) = The total momentum before an interaction.

\(p_{after}\) = The total momentum after the interaction.

Explosions

During an explosion a single object with zero momentum splits into two smaller objects.
The total momentum before the explosion is zero. Due to conservation of momentum the total momentum after the explosion is also zero.

\(p_{before} = p_{after}\)

Since

\(p = mv\)

Then:

ConservationofMomentumExplosion.png

\(0 = m_1 v_1 + m_2 v_2\)

Where

\(m_1\) = The mass of object 1.

\(v_1\) = The velocity of object 1 after the explosion.

\(m_2\) = The mass of object 2.

\(v_2\) = The velocity of object 2 after the explosion.

Explosion.gif

Example Explosion Calculations

An 80kg ice skater and a 90kg ice skater begin at rest and then push away from one another. The 80kg ice skater moves away with a velocity of 0.45m/s. Calculate the velocity of the 90kg ice skater correct to two significant figures. An 18th century cannon of mass 2000kg fires a 5.5kg cannon ball at a velocity of 180m/s. Calculate the recoil velocity of the cannon correct to two significant figures.
CofMCalc1.png
CofMCalc2.png
1. State the known quantities

pbefore = 0kgm/s

m1 = 80kg

m2 = 90kg

v1 = 0.45m/s

1. State the known quantities

pbefore = 0kgm/s

m1 = 2000kg

m2 = 5.5kg

v1 = 180m/s

2. Substitute the numbers and evaluate.

\(p_{before} = p_{after}\)

\(0 = m_1 v_1 + m_2 v_2\)

\(0 = 80 \times 0.45 + 90 \times v_2\)

\(0 = 36 + 90v_2\)

2. Substitute the numbers and evaluate.

\(p_{before} = p_{after}\)

\(0 = m_1 v_1 + m_2 v_2\)

\(0 = 2000 \times v_1 + 5.5 \times 180\)

\(0 = 2000v_1 + 990\)

3. Rearrange the equation and solve.

\(90v_2 = -36\)

\(v_2 = \frac{-36}{90}\)

\(v_2 = -0.40m/s\)

3. Rearrange the equation and solve.

\(2000v_1 = -990\)

\(v_1 = \frac{-990}{2000}\)

\(v_1 = -0.495m/s\)

\(v_1 \approx -0.50m/s\)

Elastic Collisions

During elastic collisions kinetic energy is conserved, so the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
During elastic collisions the objects bounce off one another.

\(p_{before} = p_{after}\)

Since

\(p = mv\)

Then:

ConservationofMomentumElasticCollision.png

\(m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4\)

Where

\(m_1\) = The mass of object 1.

\(v_1\) = The velocity of object 1 before the collision.

\(v_3\) = The velocity of object 1 after the collision.

\(m_2\) = The mass of object 2.

\(v_2\) = The velocity of object 2 before the collision.

\(v_4\) = The velocity of object 2 after the collision.

ElasticCollision.gif

Example Elastic Collision Calculations

A trolley of mass 3kg travels at a velocity of 4m/s before colliding with a trolley of mass 1kg travelling in the same direction with a velocity of 2m/s. After the collision the 3kg trolley is moving with a velocity of 3m/s. Calculate the velocity of the 1kg trolley after the collision. A rubber ball of mass 0.5kg travels at a speed of 4m/s towards another rubber ball, of mass 0.2kg traveling in the opposite direction with a speed of 3m/s. The 0.5kg rubber ball stops completely. Calculate the velocity of the 0.2kg rubber ball after the collision.
CofMCalc3.png
CofMCalc4.png
1. State the known quantities

m1 = 3kg

v1 = 4m/s

v3 = 3m/s

m2 = 1kg

v2 = 2m/s

1. State the known quantities

m1 = 0.5kg

v1 = 4m/s

v3 = 0m/s

m2 = 0.2kg

v2 = -3m/s This is negative because it is travelling in the opposite direction.

2. Substitute the numbers and evaluate.

\(m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4\)

\(3 \times 4 + 1 \times 2 = 3 \times 3 + 1 \times v_4\)

\(12 + 2 = 9 + v_4\)

\(14 = 9 + v_4\)

2. Substitute the numbers and evaluate.

\(m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4\)

\(0.5 \times 4 + 0.2 \times (-3) = 0.5 \times 0 + 0.2 \times v_4\)

\(2 -0.6 = 0 + 0.2v_4\)

\(1.4 = 0.2v_4\)

3. Rearrange the equation and solve.

\(v_4 = 14-9\)

\(v_4 = 5m/s\)

3. Rearrange the equation and solve.

\(v_4 = \frac{1.4}{0.2}\)

\(v_4 = 7m/s\)

Inelastic Collisions

During inelastic collisions kinetic energy is not conserved, so the total kinetic energy before is greater than the total kinetic energy after the collision.
During perfectly inelastic collisions the objects stick together.

\(p_{before} = p_{after}\)

Since

\(p = mv\)

Then

ConservationofMomentumInelasticCollision.png

\(m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3\)

Where

\(m_1\) = The mass of object 1.

\(v_1\) = The velocity of object 1 before the collision.

\(m_2\) = The mass of object 2.

\(v_2\) = The velocity of object 2 before the collision.

\(v_3\) = The velocity of new larger object after the collision.

InelasticCollision2.gif
A trolley of mass 3kg travels at a velocity of 4m/s before colliding with a trolley of mass 1kg travelling in the same direction with a velocity of 2m/s. After the collision the two trolleys stick together. Calculate the velocity of the new larger trolley after the collision. A lorry of mass 15Mg travels at a speed of 20m/s towards a car, of mass 2500kg traveling in the opposite direction at 10m/s. In this collision the two vehicles stick together. Calculate the velocity of the combined vehicles after the collision correct to two significant figures.
CofMCalc5.png
CofMCalc6.png
1. State the known quantities

m1 = 3kg

v1 = 4m/s

m2 = 1kg

v2 = 2m/s

1. State the known quantities

m1 = 15Mg = 15x103kg

v1 = 4m/s

m2 = 2.5x103kg

v2 = -10m/s This is negative because it is travelling in the opposite direction.

2. Substitute the numbers and evaluate.

\(m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3\)

\(3 \times 4 + 1 \times 2 = (3+1) \times v_3\)

\(12 + 2 = 4v_3\)

\(14 = 4v_3\)

2. Substitute the numbers and evaluate.

\(m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3\)

\(15 \times 10^3 \times 20 + 2.5 \times 10^3 \times (-10) = ((15 \times 10^3) + (2.5 \times 10^3)) \times v_3\)

\(300000 - 25000 = 17500 \times v_3\)

\(275000 = 17500v_3\)

3. Rearrange the equation and solve.

\(v_3 = \frac{14}{4}\)

\(v_3 = 3.5m/s\)

3. Rearrange the equation and solve.

\(v_3 = \frac{275000}{17500}\)

\(v_3 = 15.7142m/s\)

\(v_3 \approx 16m/s\)

References

AQA

Conservation of momentum, page 183, GCSE Combined Science Trilogy; Physics, CGP, AQA
Conservation of momentum, page 216, GCSE Physics; The Complete 9-1 Course for AQA, CGP, AQA
Conservation of momentum, pages 150-153, 156-157, GCSE Physics; Third Edition, Oxford University Press, AQA
Conservation of momentum, pages 169-70m GCSE Physics, Hodder, AQA
Conservation of momentum, pages 70, 71, GCSE Physics; The Revision Guide, CGP, AQA

Edexcel

Conservation of momentum, law of, page 309, GCSE Combined Science, Pearson Edexcel
Conservation of momentum, page 25, GCSE Physics, Pearson Edexcel
Conservation of momentum, pages 153, 154, GCSE Combined Science; The Revision Guide, CGP, Edexcel
Conservation of momentum, pages 20, 21, GCSE Physics; The Revision Guide, CGP, Edexcel
Conservation of momentum, pages 44, 45, GCSE Physics, CGP, Edexcel

OCR

Law of conservation; Momentum, pages 72, Gateway GCSE Physics, Oxford, OCR

Key Stage 5

Meaning

The law of conservation of momentum is the observation that the total momentum in a closed isolated system remains the same before and after any interaction between those particles (provided no external resultant forces acts upon that system.

About Conservation of Momentum

Formula

Total Momentum Before = Total Momentum After

\(p_{before} = p_{after}\)

Where

\(p_{before}\) = The total momentum before an interaction.

\(p_{after}\) = The total momentum after the interaction.

Explosions

During an explosion a single object with zero momentum splits into two smaller objects.
The total momentum before the explosion is zero. Due to conservation of momentum the total momentum after the explosion is also zero.

\(p_{before} = p_{after}\)

Since

\(p = mv\)

Then:

ConservationofMomentumExplosion.png

\(0 = m_1 v_1 + m_2 v_2\)

Where

\(m_1\) = The mass of object 1.

\(v_1\) = The velocity of object 1 after the explosion.

\(m_2\) = The mass of object 2.

\(v_2\) = The velocity of object 2 after the explosion.

Explosion.gif

Example Explosion Calculations

An 80kg ice skater and a 90kg ice skater begin at rest and then push away from one another. The 80kg ice skater moves away with a velocity of 0.45m/s. Calculate the velocity of the 90kg ice skater correct to two significant figures. An 18th century cannon of mass 2000kg fires a 5.5kg cannon ball at a velocity of 180m/s. Calculate the recoil velocity of the cannon correct to two significant figures.
CofMCalc1.png
CofMCalc2.png
1. State the known quantities

pbefore = 0kgm/s

m1 = 80kg

m2 = 90kg

v1 = 0.45m/s

1. State the known quantities

pbefore = 0kgm/s

m1 = 2000kg

m2 = 5.5kg

v1 = 180m/s

2. Substitute the numbers and evaluate.

\(p_{before} = p_{after}\)

\(0 = m_1 v_1 + m_2 v_2\)

\(0 = 80 \times 0.45 + 90 \times v_2\)

\(0 = 36 + 90v_2\)

2. Substitute the numbers and evaluate.

\(p_{before} = p_{after}\)

\(0 = m_1 v_1 + m_2 v_2\)

\(0 = 2000 \times v_1 + 5.5 \times 180\)

\(0 = 2000v_1 + 990\)

3. Rearrange the equation and solve.

\(90v_2 = -36\)

\(v_2 = \frac{-36}{90}\)

\(v_2 = -0.40m/s\)

3. Rearrange the equation and solve.

\(2000v_1 = -990\)

\(v_1 = \frac{-990}{2000}\)

\(v_1 = -0.495m/s\)

\(v_1 \approx -0.50m/s\)

Elastic Collisions

During elastic collisions kinetic energy is conserved, so the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
During elastic collisions the objects bounce off one another.

\(p_{before} = p_{after}\)

Since

\(p = mv\)

Then:

ConservationofMomentumElasticCollision.png

\(m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4\)

Where

\(m_1\) = The mass of object 1.

\(v_1\) = The velocity of object 1 before the collision.

\(v_3\) = The velocity of object 1 after the collision.

\(m_2\) = The mass of object 2.

\(v_2\) = The velocity of object 2 before the collision.

\(v_4\) = The velocity of object 2 after the collision.

ElasticCollision.gif

Example Elastic Collision Calculations

A trolley of mass 3kg travels at a velocity of 4m/s before colliding with a trolley of mass 1kg travelling in the same direction with a velocity of 2m/s. After the collision the 3kg trolley is moving with a velocity of 3m/s. Calculate the velocity of the 1kg trolley after the collision. A rubber ball of mass 0.5kg travels at a speed of 4m/s towards another rubber ball, of mass 0.2kg traveling in the opposite direction with a speed of 3m/s. The 0.5kg rubber ball stops completely. Calculate the velocity of the 0.2kg rubber ball after the collision.
CofMCalc3.png
CofMCalc4.png
1. State the known quantities

m1 = 3kg

v1 = 4m/s

v3 = 3m/s

m2 = 1kg

v2 = 2m/s

1. State the known quantities

m1 = 0.5kg

v1 = 4m/s

v3 = 0m/s

m2 = 0.2kg

v2 = -3m/s This is negative because it is travelling in the opposite direction.

2. Substitute the numbers and evaluate.

\(m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4\)

\(3 \times 4 + 1 \times 2 = 3 \times 3 + 1 \times v_4\)

\(12 + 2 = 9 + v_4\)

\(14 = 9 + v_4\)

2. Substitute the numbers and evaluate.

\(m_1 v_1 + m_2 v_2 = m_1 v_3 + m_2 v_4\)

\(0.5 \times 4 + 0.2 \times (-3) = 0.5 \times 0 + 0.2 \times v_4\)

\(2 -0.6 = 0 + 0.2v_4\)

\(1.4 = 0.2v_4\)

3. Rearrange the equation and solve.

\(v_4 = 14-9\)

\(v_4 = 5m/s\)

3. Rearrange the equation and solve.

\(v_4 = \frac{1.4}{0.2}\)

\(v_4 = 7m/s\)

Inelastic Collisions

During inelastic collisions kinetic energy is not conserved, so the total kinetic energy before is greater than the total kinetic energy after the collision.
During perfectly inelastic collisions the objects stick together.

\(p_{before} = p_{after}\)

Since

\(p = mv\)

Then

ConservationofMomentumInelasticCollision.png

\(m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3\)

Where

\(m_1\) = The mass of object 1.

\(v_1\) = The velocity of object 1 before the collision.

\(m_2\) = The mass of object 2.

\(v_2\) = The velocity of object 2 before the collision.

\(v_3\) = The velocity of new larger object after the collision.

InelasticCollision2.gif
A trolley of mass 3kg travels at a velocity of 4m/s before colliding with a trolley of mass 1kg travelling in the same direction with a velocity of 2m/s. After the collision the two trolleys stick together. Calculate the velocity of the new larger trolley after the collision. A lorry of mass 15Mg travels at a speed of 20m/s towards a car, of mass 2500kg traveling in the opposite direction at 10m/s. In this collision the two vehicles stick together. Calculate the velocity of the combined vehicles after the collision correct to two significant figures.
CofMCalc5.png
CofMCalc6.png
1. State the known quantities

m1 = 3kg

v1 = 4m/s

m2 = 1kg

v2 = 2m/s

1. State the known quantities

m1 = 15Mg = 15x103kg

v1 = 4m/s

m2 = 2.5x103kg

v2 = -10m/s This is negative because it is travelling in the opposite direction.

2. Substitute the numbers and evaluate.

\(m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3\)

\(3 \times 4 + 1 \times 2 = (3+1) \times v_3\)

\(12 + 2 = 4v_3\)

\(14 = 4v_3\)

2. Substitute the numbers and evaluate.

\(m_1 v_1 + m_2 v_2 = (m_1 + m_2) v_3\)

\(15 \times 10^3 \times 20 + 2.5 \times 10^3 \times (-10) = ((15 \times 10^3) + (2.5 \times 10^3)) \times v_3\)

\(300000 - 25000 = 17500 \times v_3\)

\(275000 = 17500v_3\)

3. Rearrange the equation and solve.

\(v_3 = \frac{14}{4}\)

\(v_3 = 3.5m/s\)

3. Rearrange the equation and solve.

\(v_3 = \frac{275000}{17500}\)

\(v_3 = 15.7142m/s\)

\(v_3 \approx 16m/s\)

Retrieved from "https://keystagewiki.com/index.php?title=Conservation_of_Momentum&oldid=23492"