Difference between revisions of "GCSE Physics Required Practical: Investigating Newton's Second Law"
(→Method) |
|||
| Line 23: | Line 23: | ||
#Release the [[weight]] and allow the glider to [[accelerate]]. | #Release the [[weight]] and allow the glider to [[accelerate]]. | ||
#Record the [[velocity]] through [[Light Gate|light gates]] 1 and 2 and the [[time]] taken between [[Light Gate|light gates]]. | #Record the [[velocity]] through [[Light Gate|light gates]] 1 and 2 and the [[time]] taken between [[Light Gate|light gates]]. | ||
| − | #Use the equation <math>a=\frac{v-u}{t}</math> to calculate the [[acceleration]] of the | + | #Use the equation <math>a=\frac{v-u}{t}</math> to calculate the [[acceleration]] of the glider. |
#Repeat steps 3-6 adding 0.1N [[weight]] up to around 0.6N. | #Repeat steps 3-6 adding 0.1N [[weight]] up to around 0.6N. | ||
| − | #Plot a [[graph]] with the [[force]] of [[weight]] on the [[x-axis]] and the [[acceleration]] on the [[y-axis]]. The [[gradient]] of this [[graph]] will be the [[mass]] of the | + | #Plot a [[graph]] with the [[force]] of [[weight]] on the [[x-axis]] and the [[acceleration]] on the [[y-axis]]. The [[gradient]] of this [[graph]] will be the [[mass]] of the glider showing that <math>F=ma</math>. |
#Measure the [[mass]] of the glider using an [[Electronic Balance|electronic balance]] to compare results. | #Measure the [[mass]] of the glider using an [[Electronic Balance|electronic balance]] to compare results. | ||
| Line 57: | Line 57: | ||
#Release the [[weight]] and allow the glider to [[accelerate]]. | #Release the [[weight]] and allow the glider to [[accelerate]]. | ||
#Record the [[velocity]] through [[Light Gate|light gates]] 1 and 2. | #Record the [[velocity]] through [[Light Gate|light gates]] 1 and 2. | ||
| − | #Use the equation <math>v^2 - u^2=2as</math> to calculate the [[acceleration]] of the | + | #Use the equation <math>v^2 - u^2=2as</math> to calculate the [[acceleration]] of the glider. |
#Repeat steps 4-7 adding 0.1N [[weight]] up to around 0.6N. | #Repeat steps 4-7 adding 0.1N [[weight]] up to around 0.6N. | ||
| − | #Plot a [[graph]] with the [[force]] of [[weight]] on the [[x-axis]] and the [[acceleration]] on the [[y-axis]]. The [[gradient]] of this [[graph]] will be the [[mass]] of the | + | #Plot a [[graph]] with the [[force]] of [[weight]] on the [[x-axis]] and the [[acceleration]] on the [[y-axis]]. The [[gradient]] of this [[graph]] will be the [[mass]] of the glider showing that <math>F=ma</math>. |
#Measure the [[mass]] of the glider using an [[Electronic Balance|electronic balance]] to compare results. | #Measure the [[mass]] of the glider using an [[Electronic Balance|electronic balance]] to compare results. | ||
| Line 69: | Line 69: | ||
====Improving [[Precision]]==== | ====Improving [[Precision]]==== | ||
: Calculate the [[weight]] added correct to two [[Significant Figure|significant figures]] by [[measure|measuring]] its [[mass]] to two [[Significant Figures|significant figures]] each time and using the equation <math>W=mg</math> with <math>g=9.8</math>. This will give a more [[precise]] knowledge of the [[weight]] rather than relying on the number printed on the [[weight]]s which may be [[precise]] to only one [[Significant Figure|significant figure]]. | : Calculate the [[weight]] added correct to two [[Significant Figure|significant figures]] by [[measure|measuring]] its [[mass]] to two [[Significant Figures|significant figures]] each time and using the equation <math>W=mg</math> with <math>g=9.8</math>. This will give a more [[precise]] knowledge of the [[weight]] rather than relying on the number printed on the [[weight]]s which may be [[precise]] to only one [[Significant Figure|significant figure]]. | ||
| − | : Use a ruler with a higher [[resolution]] to give a more [[precise]] [[displacement]] for the [[glider]]. | + | : Use a ruler with a higher [[resolution]] to give a more [[precise]] [[displacement]] for the glider. |
| + | |||
| + | ===Experiment 2: Trolley with Markings=== | ||
| + | ====Variables==== | ||
| + | : [[Independent Variable]]: The [[force]] applied to the [[object]]. | ||
| + | : [[Dependent Variable]]: The [[acceleration]] of the [[object]]. | ||
| + | : [[Control Variable]]s: The [[mass]] of the [[object]]. | ||
| + | |||
| + | ====Method==== | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | |[[File:RequiredPracticalFMA3.png|center|600px]] | ||
| + | |- | ||
| + | | style="height:20px; width:200px; text-align:center;" |A [[diagram]] of the [[apparatus]] used to investigate the effect of a [[force]] on the [[acceleration]] of an [[object]]. | ||
| + | |} | ||
| + | |||
| + | : Set up the equipment as shown in the [[diagram]]. | ||
| + | #Adjust the [[gradient]] of the slope so that once pushed the trolley will move with a constant [[velocity]]. | ||
| + | #Attach a known [[weight]] (approximately 0.1N) to wire. | ||
| + | #Release the [[weight]] and start the [[stopwatch]] allowing the trolley to [[accelerate]]. | ||
| + | #Record the [[time]] on the [[stopwatch]] at each 10cm marker. | ||
| + | #Calculate the [[time]] difference between each 10cm marker. | ||
| + | #Use the equation <math>v=s/t</math> to calculate the [[Mean Average|average]] [[velocity]] between each 10cm marker. | ||
| + | #Use the equation <math>a=\frac{v-u}{t}</math> to calculate the [[acceleration]] of the trolley. | ||
| + | #Repeat steps 2-7 adding 0.1N [[weight]] up to around 0.6N. | ||
| + | #Plot a [[graph]] with the [[force]] of [[weight]] on the [[x-axis]] and the [[acceleration]] on the [[y-axis]]. The [[gradient]] of this [[graph]] will be the [[mass]] of the glider showing that <math>F=ma</math>. | ||
| + | #Measure the [[mass]] of the trolley using an [[Electronic Balance|electronic balance]] to compare [[results]]. | ||
| + | |||
| + | ====Improving [[Accuracy]]==== | ||
| + | : Calculate the [[weight]] added by [[measure|measuring]] its [[mass]] each time and using the equation <math>W=mg</math> with <math>g=9.8</math>. This will give a more [[accuracy|accurate]] knowledge of the [[weight]] rather than relying on the number printed on the [[weight]]s. | ||
| + | : Adjust the [[friction]] compensated slope so that the trolley will move at constant [[velocity]] when no [[Unbalanced Force|unbalanced force]] is applied. | ||
| + | : [[Lubricate]] the [[pulley]] to reduce the [[force]] of [[friction]] which acts against the [[weight]] added. | ||
| + | : Use [[Light Gate|light gates]] and a [[Data Logger|data logger]] to record the [[time]] taken between each marker. | ||
| + | : Use a smaller [[weight]] so that the trolley moves more slowly allowing the timing to be more [[accurate]]. | ||
| + | |||
| + | ====Improving [[Precision]]==== | ||
| + | : Calculate the [[weight]] added correct to two [[Significant Figure|significant figures]] by [[measure|measuring]] its [[mass]] to two [[Significant Figures|significant figures]] each time and using the equation <math>W=mg</math> with <math>g=9.8</math>. This will give a more [[precise]] knowledge of the [[weight]] rather than relying on the number printed on the [[weight]]s which may be [[precise]] to only one [[Significant Figure|significant figure]]. | ||
| + | : Use [[Light Gate|light gates]] and a [[Data Logger|data logger]] to record the [[time]] taken between each marker. | ||
Revision as of 14:30, 19 March 2019
Contents
Key Stage 4
Meaning
Investigate the relationship between the force and acceleration of an object.
Experiment 1a: Light Gates Measuring Time and Velocity
Variables
- Independent Variable: The force applied to the object.
- Dependent Variable: The acceleration of the object.
- Control Variables: The mass of the object.
Method
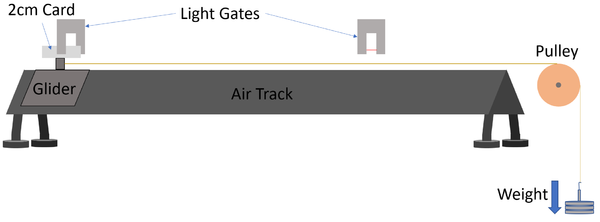
| A diagram of the apparatus used to investigate the effect of a force on the acceleration of an object. |
- Set up the equipment as shown in the diagram.
- Program into the light gates the length of the card on the glider as 2cm.
- Set the light gates to record the velocity through the gate and the time taken to travel between gates.
- Attach a known weight (approximately 0.1N) to wire.
- Release the weight and allow the glider to accelerate.
- Record the velocity through light gates 1 and 2 and the time taken between light gates.
- Use the equation \(a=\frac{v-u}{t}\) to calculate the acceleration of the glider.
- Repeat steps 3-6 adding 0.1N weight up to around 0.6N.
- Plot a graph with the force of weight on the x-axis and the acceleration on the y-axis. The gradient of this graph will be the mass of the glider showing that \(F=ma\).
- Measure the mass of the glider using an electronic balance to compare results.
Improving Accuracy
- Calculate the weight added by measuring its mass each time and using the equation \(W=mg\) with \(g=9.8\). This will give a more accurate knowledge of the weight rather than relying on the number printed on the weights.
- Ensure the glider remains motionless when no weight is attached. If the glider moves then adjust the feet on the air track until the glider remains stationary.
- Lubricate the pulley to reduce the force of friction which acts against the weight added.
Improving Precision
- Calculate the weight added correct to two significant figures by measuring its mass to two significant figures each time and using the equation \(W=mg\) with \(g=9.8\). This will give a more precise knowledge of the weight rather than relying on the number printed on the weights which may be precise to only one significant figure.
Experiment 1b: Light Gates Measuring Displacement and Velocity
Variables
- Independent Variable: The force applied to the object.
- Dependent Variable: The acceleration of the object.
- Control Variables: The mass of the object.
Method
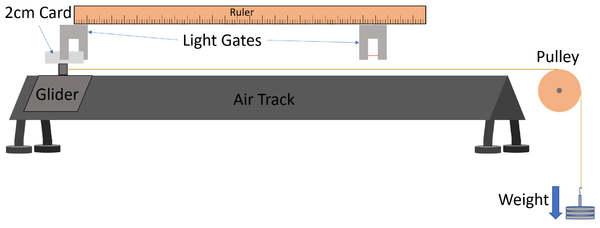
| A diagram of the apparatus used to investigate the effect of a force on the acceleration of an object. |
- Set up the equipment as shown in the diagram.
- Program into the light gates the length of the card on the glider as 2cm.
- Set the light gates to record the velocity through the gate.
- Measure and record the distance between the light gates using a ruler. This will be the displacement of the glider.
- Attach a known weight (approximately 0.1N) to wire.
- Release the weight and allow the glider to accelerate.
- Record the velocity through light gates 1 and 2.
- Use the equation \(v^2 - u^2=2as\) to calculate the acceleration of the glider.
- Repeat steps 4-7 adding 0.1N weight up to around 0.6N.
- Plot a graph with the force of weight on the x-axis and the acceleration on the y-axis. The gradient of this graph will be the mass of the glider showing that \(F=ma\).
- Measure the mass of the glider using an electronic balance to compare results.
Improving Accuracy
- Calculate the weight added by measuring its mass each time and using the equation \(W=mg\) with \(g=9.8\). This will give a more accurate knowledge of the weight rather than relying on the number printed on the weights.
- Ensure the glider remains motionless when no weight is attached. If the glider moves then adjust the feet on the air track until the glider remains stationary.
- Lubricate the pulley to reduce the force of friction which acts against the weight added.
Improving Precision
- Calculate the weight added correct to two significant figures by measuring its mass to two significant figures each time and using the equation \(W=mg\) with \(g=9.8\). This will give a more precise knowledge of the weight rather than relying on the number printed on the weights which may be precise to only one significant figure.
- Use a ruler with a higher resolution to give a more precise displacement for the glider.
Experiment 2: Trolley with Markings
Variables
- Independent Variable: The force applied to the object.
- Dependent Variable: The acceleration of the object.
- Control Variables: The mass of the object.
Method
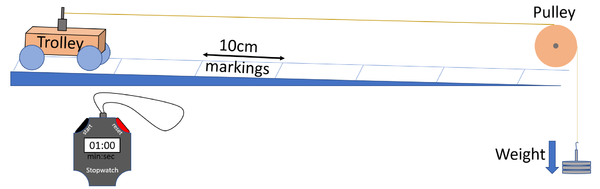
| A diagram of the apparatus used to investigate the effect of a force on the acceleration of an object. |
- Set up the equipment as shown in the diagram.
- Adjust the gradient of the slope so that once pushed the trolley will move with a constant velocity.
- Attach a known weight (approximately 0.1N) to wire.
- Release the weight and start the stopwatch allowing the trolley to accelerate.
- Record the time on the stopwatch at each 10cm marker.
- Calculate the time difference between each 10cm marker.
- Use the equation \(v=s/t\) to calculate the average velocity between each 10cm marker.
- Use the equation \(a=\frac{v-u}{t}\) to calculate the acceleration of the trolley.
- Repeat steps 2-7 adding 0.1N weight up to around 0.6N.
- Plot a graph with the force of weight on the x-axis and the acceleration on the y-axis. The gradient of this graph will be the mass of the glider showing that \(F=ma\).
- Measure the mass of the trolley using an electronic balance to compare results.
Improving Accuracy
- Calculate the weight added by measuring its mass each time and using the equation \(W=mg\) with \(g=9.8\). This will give a more accurate knowledge of the weight rather than relying on the number printed on the weights.
- Adjust the friction compensated slope so that the trolley will move at constant velocity when no unbalanced force is applied.
- Lubricate the pulley to reduce the force of friction which acts against the weight added.
- Use light gates and a data logger to record the time taken between each marker.
- Use a smaller weight so that the trolley moves more slowly allowing the timing to be more accurate.
Improving Precision
- Calculate the weight added correct to two significant figures by measuring its mass to two significant figures each time and using the equation \(W=mg\) with \(g=9.8\). This will give a more precise knowledge of the weight rather than relying on the number printed on the weights which may be precise to only one significant figure.
- Use light gates and a data logger to record the time taken between each marker.