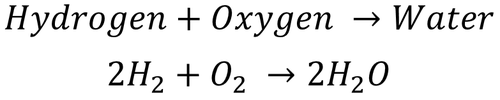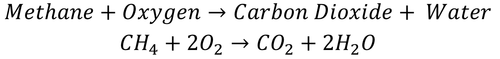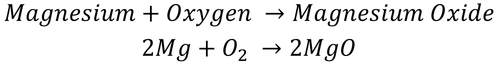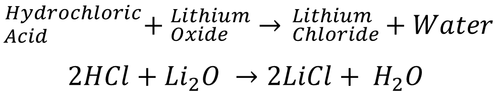Balanced Symbol Equation

Key Stage 3

Meaning

A Balanced Symbol Equation is a way to show the reactants and products in a chemical reaction using the chemical formulae of the reactants and products.

About Balanced Symbol Equations

Balanced Symbol Equations shows the number of molecules of each chemical and the numbers of each atom within those chemicals.

Balanced Symbol Equations can be used to find the quantity of each chemical needed to have a complete chemical reaction.

The Word Equation has been given above each Balanced Symbol Equation.

This shows there are two H₂ molecules and one O₂ molecule needed to make two molecules of H₂O.

This shows there is one CH₄ molecule and two O₂ molecules needed to make one molecule of CO₂ and two molecules of H₂O.

This shows there are two atoms of Mg and one molecule of O₂ needed to make two molecules of MgO.

This shows there are two HCl molecules and one Li₂O molecule needed to make two molecules of LiCl and one molecule of H₂O.

Balancing Equations

You may know the chemical formulae of the reactants and products but not know the number of each chemical needed. For that you must balance the equation.

To balance and equation you need the same number of each type of atom on the left as you do on the right.

Lithium + Fluorine → Lithium Fluoride
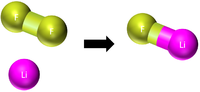
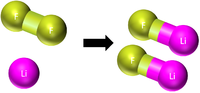
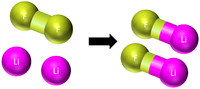
Step 1	Step 2	Step 3

_Li + _F₂ → _LiF Reactants = Products 1Li = 1Li 2F ≠ 1F We need 2 Fluorine atoms in the products.	_Li + _F₂ → 2LiF Reactants = Products 1Li ≠ 2Li 2F = 2F There are now too many Lithium atoms in the products so we need 2 in the reactants.	2Li + _F₂ → 2LiF Reactants = Products 2Li = 2Li 2F = 2F This equation is balanced: 2Li + F₂ → 2LiF

Aluminium + Chlorine → Aluminium Chloride

_Al + _Cl₂ → _AlCl₃

Reactants = Products

1Al = 1Al

2Cl ≠ 3Cl

We need the same number of Chlorine atoms on both sides. To do that we can find the Lowest Common Multiple. In this case it is 6, so we times the left 2 Chlorines by 3 and the right 3 Chlorines by 2.

_Al + 3Cl₂ → 2AlCl₃

Reactants = Products

1Al ≠ 2Al

6Cl = 6Cl

There are now too many Aluminium atoms on the right, so we need to multiply the left Aluminium by 2.

2Al + 3Cl₂ → 2AlCl₃

Reactants = Products

2Al = 2Al

6Cl = 6Cl

This equation is now balanced: 2Al + 3Cl₂ → 2AlCl₃

Aluminium + Oxygen → Aluminium Oxide

_Al + _O₂ → _Al₂O₃

Reactants = Products

1Al ≠ 2Al

2O ≠ 3O

We need the same number of Oxygen atoms on both sides. To do that we can find the Lowest Common Multiple. In this case it is 6, so we times the left 2 Oxygens by 3 and the right 3 Oxygens by 2.

_Al + 3O₂ → 2Al₂O₃

Reactants = Products

1Al ≠ 4Al

6O = 6O

The Oxygen atoms are now balanced but the Aluminium atoms are not. We need 4 times as many Aluminium atoms on the left.

4Al + 3O₂ → 2Al₂O₃

Reactants = Products

4Al = 4Al

6O = 6O

This equation is now balanced: 4Al + 3O₂ → 2Al₂O₃

Key Stage 4

Meaning

A Balanced Symbol Equation is a way to show the reactants and products in a chemical reaction using the chemical formulae of the reactants and products.

About Balanced Symbol Equations

Balanced Symbol Equations show the number of molecules of each chemical and the numbers of each atom within those chemicals.

Balanced Symbol Equations can be used to find the quantity of each chemical needed to have a complete chemical reaction.

Examples

2H₂(g) + O₂(g) → 2H₂O(l)

C₂H₄(g) + Br₂(g) → C₂H₄Br₂(g)

C₆H₁₂O₆(s) + 6O₂(g) → 6H₂O(l) + 6CO₂(g)

4Al(s) + 3O₂(g) → 2Al₂O₃(s)

Calculating the Mass Required for a Complete Reaction

Find the mass of Oxygen needed to completely oxidise all of the Magnesium: 2Mg + O₂ → 2MgO 48g + x = y	Find the mass of Oxygen needed for the complete combustion of Methane. CH₄ + 2O₂ → 2H₂O + CO₂ 32g + x = y	Find the mass of Hydrochloric Acid needed to completely neutralise all of the Sodium Hydroxide. NaOH + HCl → NaCl + H₂O 20g + x = y + z
Find the Relative Formula Mass of the reactants. M_r of Mg = 24g M_r of O₂ = 16x2 M_r of O₂ = 32g	Find the Relative Formula Mass of the reactants. M_r of CH₄ = 16g M_r of O₂ = 16x2 M_r of O₂ = 32g	Find the Relative Formula Mass of the reactants. M_r of NaOH = 40g M_r of HCl = 36.5g
State the ratio of moles of each chemical needed. 2 moles of Mg are needed for every 1 mole of O₂	State the ratio of moles of each chemical needed. 1 mole of CH₄ is needed for every 2 moles of O₂	State the ratio of moles of each chemical needed. 1 mole of HCl are needed for every 1 mole of NaOH
Find the number of moles supplied of the known mass. No. Moles = \(\frac{Mass}{M_r}\) No. Moles = \(\frac{48}{24}\) No. Moles = 2 Mole Therefore 1 mole of O₂ is needed. 1 mole of O₂ = 32g	Find the number of moles supplied of the known mass. No. Moles = \(\frac{Mass}{M_r}\) No. Moles = \(\frac{32}{16}\) No. Moles = 2 Mole Therefore 4 moles of O₂ are needed. 4 moles of O₂ = 128g	Find the number of moles supplied of the known mass. No. Moles = \(\frac{Mass}{M_r}\) No. Moles = \(\frac{20}{40}\) No. Moles = 0.5 Mole Therefore 0.5 mole of HCl is needed. 0.5 mole of HCl = 18.25g

Limiting Reactants

A limiting reactant is a reactant that is not supplied in a large enough quantity for a complete reaction with the other reactants.

2H₂(g) + O₂(g) → 2H₂O(l)

If there is 4g of Hydrogen then 32g of Oxygen is needed for a complete reaction to occur.

If there is 4g of Hydrogen but only 31g of Oxygen then the Oxygen is a limiting reactant.

If there is 3g of Hydrogen but only 32g of Oxygen then the Hydrogen is a limiting reactant.

If there are are 6g of Carbon and 15g of Oxygen in the following reaction: C + O₂ → CO₂ Which is the limiting reactant in this reaction?	If there are are 27g of Aluminium and 32g of Oxygen in the following reaction: 4Al + 3O₂ → 2Al₂O₃ Which is the limiting reactant in this reaction?	If there are are 180g of Glucose and 200g of Oxygen in the following reaction: C₆H₁₂O₆ + 6O₂ → 6H₂O + 6CO₂ Which is the limiting reactant in this reaction?
Find the Relative Formula Mass of the reactants. M_r of C = 12g M_r of O₂ = 32g	Find the Relative Formula Mass of the reactants. M_r of NaOH = 40g M_r of HCl = 36.5g	Find the Relative Formula Mass of the reactants. M_r of NaOH = 40g M_r of HCl = 36.5g
State the ratio of moles of each chemical needed. 1 moles of C is needed for every 1 mole of O₂	State the ratio of moles of each chemical needed. 4 moles of Al are needed for every 3 moles of O₂	State the ratio of moles of each chemical needed. 1 mole of C₆H₁₂O₆ is needed for every 6 moles of O₂
Find the number of moles supplied of each chemical. No. Moles of C = \(\frac{Mass}{M_r}\) No. Moles of C = \(\frac{6}{12}\) No. Moles = 0.5 mol Therefore 0.5 moles of O₂ is needed. No. Moles of O = \(\frac{Mass}{M_r}\) No. Moles of O = \(\frac{15}{32}\) No. Moles = 0.46 mol Oxygen is the limiting reactant. 1 mole of O₂ = 32g	Find the number of moles supplied of each chemical. No. Moles of Al = \(\frac{Mass}{M_r}\) No. Moles of Al = \(\frac{27}{27}\) No. Moles = 1 mol Therefore 0.75 moles of O₂ are needed. No. Moles of O = \(\frac{Mass}{M_r}\) No. Moles of O = \(\frac{32}{32}\) No. Moles = 1 mol Oxygen is the limiting reactant.	Find the number of moles supplied of each chemical. No. Moles of C₆H₁₂O₆ = \(\frac{Mass}{M_r}\) No. Moles of C₆H₁₂O₆ = \(\frac{180}{180}\) No. Moles = 1 mol Therefore 6 moles of O₂ are needed. No. Moles of O = \(\frac{Mass}{M_r}\) No. Moles of O = \(\frac{200}{32}\) No. Moles = 6.25 mol Glucose is the limiting reactant.

Balancing Equations

You may know the chemical formulae of the reactants and products but not know the number of each chemical needed. For that you must balance the equation.

To balance and equation you need the same number of each type of atom on the left as you do on the right.

Magnesium Fluoride + Potassium → Potassium Fluoride + Magnesium
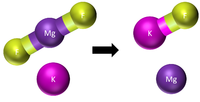
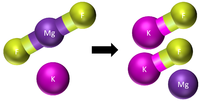
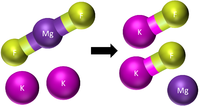
Step 1	Step 2	Step 3

_MgF₂ + _K → _KF + _Mg Reactants = Products 1Mg = 1Mg 2F ≠ 1F 1K = 1K We need 2 Fluorine atoms in the products.	_MgF₂ + _K → 2KF + _Mg Reactants = Products 1Mg = 1Mg 2F = 2F 1K ≠ 2K There are now too many Potassium atoms in the products so we need 2 in the reactants.	_MgF₂ + 2K → 2KF + _Mg Reactants = Products 1Mg = 1Mg 2F = 2F 2K = 2K This equation is balanced: MgF₂ + 2K → 2KF + Mg

Balancing Equations with Ions

If the charge on an ion is known, this information can be used to find the chemical formula of an ionic compound and be used to balance a symbol equation.

Group 1 Elements all form +1 ions; Li⁺¹, Na⁺¹, K⁺¹

Group 2 Elements all form +2 ions; Be⁺², Mg⁺², Ca⁺²

Group 3 Elements all form +3 ions; Al⁺³

Transition Metal Elements can form different ions which are shown by Roman Numerals;

Iron can form Fe (II) which is Fe⁺² or Fe (III) is Fe⁺³, Manganese can form Mn (II) which is Mn⁺² or Mn (IV) which is Mn⁺⁴

Group 5 Elements all form -3 ions; N^-3, P^-3

Group 6 Elements all form -2 ions; O^-2, S^-2

Group 7 Elements all form -1 ions; F^-1, Cl^-1

Some covalent compounds can form negative ions;

Carbonate forms -2 ions CO₃^-2

Sulphate forms -2 ions SO₄^-2

Nitrate forms -1 ions NO₃^-1

Group 1 with Group 5	Group 3 with Group 6	Sulphates and Carbonates with Group 2
Since Group 1 forms +1 ions and Group 5 forms -3 ions there will be 3 Group 1 ions for each Group 5 ion.	Since Group 3 forms +3 ions and Group 6 forms -2 ions there will be 2 Group 3 ions for every 3 Group 6 ions.	Sulphate ions and Carbonate ions both have a charge of -2 while Group 2 ions have a charge of +2 so there will be 1 Sulphate or Carbonate for every 1 Group 2 ion.
Examples Li₃N Na₃P	Examples B₂S₃ Al₂O₃	Examples MgSO₄ CaCO ₃